(Given ${\Delta _{fus}}H = 6\, kJ\, mol^{-1}$ at $0\,^oC$,
$C_p(H_2O, l) =75.3\, J\, mol^{-1} \, K^{-1}$ ,
$C_p(H_2O, s) = 36.8\, J\, mol^{-1} \, K^{ -1}$ )
In order to calculate the enthalpy change for \(H_2O\) at \(5\,^oC\) to ice at \(-\,5\,^oC\) , we need to calculated the enthalpy change of all the transformation involved in the process.
\((a)\) Energy change of \(1\,mol\), \(H_2O\,(l)\), at \(5\,^oC\)
\(\to \,1\,mol\), \(H_2O\,(l)\) , \(0\,^oC\)
\((b)\) Energy change of \(1\,mol\), \(H_2O\,(l)\), at \(0\,^oC\)
\(\to \,1\,mol\), \(H_2O\,(s)\) (ice) , \(0\,^oC\)
\((c)\) Energy change of \(1\,mol\), Ice \((s)\), at \(0\,^oC\)
\(\to \,1\,mol\), Ice \((s)\) , \(-5\,^oC\)
Total \(\Delta H\)
\( = \,{C_P}\,[{H_2}O\,(l)]\,\,\Delta T\,\, + \,\Delta H\) freezing \( + \,\,{C_P}\,[{H_2}O\,(s)]\,\,\Delta T\)
\( = \,(75.3\,\,J\,\,mo{l^{ - 1}}\,{K^{ - 1}})\,( - 5)\,K\, + ( - \,6\, \times \,{10^3}\,\,J\,mo{l^{ - 1}}\,{K^{ - 1}})\) \(+ \,(36.8\,\,J\,mo{l^{ - 1}}\,{K^{ - 1}})\,( - 5)\,K\)
\(\Delta H\,\, = \,\, - \,6.56\,\,kJ\,mo{l^{ - 1}}\) (exothermic process)
So, \(\Delta H\,\, = \,\,6.56\,\,kJ\,mo{l^{ - 1}}\)
Download our appand get started for free
Similar Questions
- 1$300\,K$ એ $C_6H_5COOH_{(s}), CO_{2(g)}$ અને $H_2O_{(l)}$ ની પ્રમાણિત નિર્માણ એન્થાલ્પી અનુક્રમે $-408, -393$ અને $-286\, kJ \,mol^{-1}$ છે. તો અચળ કદે બેન્ઝોઈક એસિડની દહન ઉષ્મા કેટલા .....$kJ$ થાય ?$(R = 8.31 \,J \,mol^{-1}\,K^{-1})$View Solution
- 2View Solution........ માટે એન્ટ્રોપીનો ફેરફાર ઋણ હોય છે.
- 3હિરાના કાર્બનની સંક્રાંતિથી ગ્રેફાઈટના કાર્બનનું બનવા માટે $\Delta$ $H - 453.5$ કેલરી છે જે શું દર્શાવે છે ?View Solution
- 4View Solutionનીચેના પૈકી કઇ પ્રક્રિયા સ્વયંભૂ નથી ?
- 5View Solutionસમોષ્મી પ્રક્રિયા માટે નીચેનામાંથી કયો સંબંધ સાચો છે ?
- 6View Solutionનીચેનામાંથી કઈ ઉષ્માશોષક પ્રક્રિયા સ્વયંભૂ છે
- 7View Solutionનીચેના પૈકી કયો અવસ્થા વિધેય નથી ?
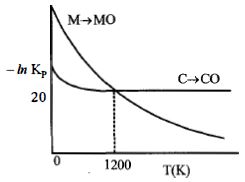
- 8નીચેનો આલેખ એ પ્રક્રિયાઓ $M(s) + \frac{1}{2}{O_2}(s)\, \to \,MO(s)\,$ અને $C(s) + \frac{1}{2}{O_2}(g)\, \to \,CO(s)\,$ માટે $- In\,K_p$ વિરુદ્ધ તાપમાનનો ફેરફાર દર્શાવે છે. તો સાયુ વિધાને ઓળખો.View Solution
- 9ગ્લુકોઝનું કેલોરીફીક મૂલ્ય ......$KJ$View Solution
$C_6H_{12}O_6 + 6O_2 \rightarrow 6CO_2 + 6H_2O ; \Delta H = -2900 \,KJ/mole $
- 10$298\, K$ તાપમાને કાર્બન મોનોક્સાઇડનું તેના તત્ત્વોમાંથી સર્જન થાય ત્યારે $(\Delta H- \Delta U) =$ .............. $\mathrm{J\,mol}^{-1}$ $(R = 8.314\,J\,K^{-1}\,mol^{-1})$View Solution
