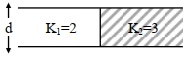
\(\mathrm{C}_{\mathrm{eq}}=\mathrm{C}_1+\mathrm{C}_2\)
\(\mathrm{C}_1=\frac{2 \epsilon_0 \mathrm{~A}}{2 \times \mathrm{d}}=10 \mu \mathrm{F}\)
\(\mathrm{C}_2=\frac{3 \epsilon_0 \mathrm{~A}}{2 \mathrm{~d}}=15 \mu \mathrm{F}\)
\(\mathrm{C}_{\mathrm{eq}}=25 \mu \mathrm{F}\)
Now the charge on
\(\mathrm{C}_1=10 \mathrm{~V} \mu \mathrm{c}\)
\(\mathrm{C}_2=1.5 \mathrm{~V} \mu \mathrm{C}.\)
Now force between the plates \(\left[\mathrm{F}=\frac{\mathrm{Q}^2}{2 \mathrm{~A} \epsilon_0}\right]\)
\(\frac{100 \mathrm{~V}^2 \times 10^{-12}}{2 \times 2 \times 10^{-4} \epsilon_0}+\frac{225 \mathrm{~V}^2 \times 10^{-12}}{2 \times 2 \times 10^{-4} \times \epsilon_0}=8\)
\(325 \mathrm{~V}^2=8 \times 4 \times 10^{-4} \times 8.85\)
\(\mathrm{~V}^2-\frac{32 \times 8.85 \times 10^{-4}}{325}\)
\(\therefore \mathrm{V}=\sqrt{\frac{283.2 \times 10^{-4}}{325}}\)
\(\mathrm{~V}=0.93 \times 10^{-2}\)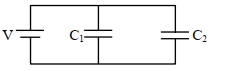
Download our appand get started for free
Similar Questions
- 1$C$ અને $3C$ સંધારકતા ધરાવતા બે સમાંતર પ્લેટ સંધારકોને સમાંતરમાં જોડવામાં આવ્યા છે અને $18\,V$ના સ્થિતિમાનના તફાવતથી તેમને વિદ્યુતભારીત કરવામાં આવે છે. હવે બેટરીને દૂર કરવામાં આવે છે અને $C$ સંધારકતા ધરાવતા સંધારકની પ્લેટો વચ્ચેની સંપૂર્ણ જગ્યામાં $9$ જેટલો ડાયઈલેકટ્રીક વચ્ચેનો અંતિમ સ્થિતિમાનનો તફાવત $\dots\dots\,V$છે.View Solution
- 2સાદા લોલકને બે પ્લેટ વચ્ચે આવર્તકાળ $T_o$ છે.હવે,પ્લેટને વિદ્યુતભારિત કરતાં આવર્તકાળ $T$ છે.તો $\frac{T}{T_o}=$View Solution
- 3બે હવા ભરેલા ભરેલા $C$ અને $nC$ કેપેસીટન્સ ધરાવતા સમાંતર પ્લેટ કેપેસીટરને $V$ વોલ્ટની બેટરી સાથે સમાંતરમાં જોડેલા છે.જ્યારે કેપેસીટર સંપૂર્ણ રીતે ચાર્જ થાય ત્યારે બેટરી દૂર કરીને પહેલા કેપેસીટરની પ્લેટ વચ્ચે $K$ ડાયઈલેક્ટ્રિક અચળાંક ધરાવતો પદાર્થ ભરવામાં આવે છે.હવે આ તંત્રનો નવો વિદ્યુતસ્થિતિમાનનો તફાવત કેટલો થાય?View Solution
- 4નીચે બે વિધાનો આપેેલા છે. એકને કથન $(A)$ અને બીજાને કારણ $(R)$ રજુ કરેલ છે.View Solution
કથન $(A):$ બે ધાત્વીય ગોળાઓને સમાન સ્થિતિમાનથી વીજભારિત કરવામાં આવેલ છે. તેમાનો એક પોલો અને બીજો ઘન છે, પરંતુ બંનેની ત્રિજ્યા સમાન છે. ઘન ગોળા પર પોલા ગોળા કરતા ઓછો વિદ્યુતભાર હશે.
કારણ $(R):$ ધાતુના ગોળાની સંઘારકતા ગોળાઓની ત્રિજ્યા ઉપર આધારિત છે.
ઉપરનાં વિધાનોનાં સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાયો ઉત્તર પસંદ કરો.
- 5$100\, W$ બલ્બથી $3\;m$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતા $E$ છે. $60\, W$ બલ્બથી $3\;m$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતા $\sqrt{\frac{x}{5}} E$ હોય તો તો $x$નું મૂલ્ય કેટલું હશે?View Solution
- 6View Solutionબે એકસમાન સંઘારકોને(કેપેસીટર) પ્રથમ શ્રેણીમાં અને ત્યારબાદ સમાંતરમાં જોડવામાં આવે છે. આ બે કિસ્સાઓમાં સમતુલ્ય સંઘારક્તાઓનો(કેપેસીટન્સ) ગુણોત્તર .......... હશે.
- 7$20\,\mu F$ ના કેપેસીટરને $500\;volts$ વડે ચાર્જ કરીને બીજા $10\,\mu F$ કેપેસીટર જેને $200\;volts$ વડે ચાર્જ કરેલ છે તેની સાથે સમાંતરમાં જોડેલ છે. તો બંને વચ્ચેનો સામાન્ય વિદ્યુતસ્થિતિમાન કેટલા $volts$ હશે?View Solution
- 8એકસમાન રેખીય ઘનતા ધરાવતા તારથી $r_0$ અંતરે એક બિંદુવત ધન વિજભારને મુક્ત કરવામાં આવે છે.આ બિંદુવત વિજભારનો વેગ $(v)$ તાત્ક્ષણિક અંતર $r$ પર કેવી રીતે આધાર રાખે?View Solution
- 9એક સમાંતર પ્લેટો ધરાવતા સંધારકમાં પ્લેટનું ક્ષેત્રફળ $40\,cm ^2$ અને તેમની વચ્યેનું અંતર $2\,mm$ છે. પ્લેટો વચ્યેના વિસ્તારમાં $1\,mm$ જાડાઈ અને $5$ જેટલો ડાઈઈલેકિટ્રક અચળાંક ધરાવતો અવાહક મૂકવામાં આવે છે. તંત્રની સંધારકતા $...........$ થશે.View Solution
- 10સમાંતર પ્લેટ કેપેસિટરની પ્લેટોનું ક્ષેત્રફળ $A$ છે. અને પ્લેટો વચ્ચેનું અંતર $100\, mm$ છે. તેમાં બે ડાઈ ઈલેકટ્રીક સ્તરો છે. એક $10$ ડાઈ ઈલેકટ્રીક અચળાંક અને $6\, mm$ જાડાઈ ધરાવતું અને બીજુ $5$ ડાઈ ઈલેકટ્રીક અચળાંક અને $4\, mm$ જાડાઈ ધરાવતું છે. તો કેપેસિટરની કેપેસિટન્સ શોધો.View Solution
