$100\, m ^{2}$ ક્ષેત્રફળ અને $10\, m$ બે પ્લેટ વચ્ચેનું અંતર ધરાવતાં સમાંતર પ્લેટ કેપેસિટર છે,તેમાં $5\,m$માં ડાઇઇલેક્ટ્રીક અચળાંક $10$ ધરાવતા ડાઇઇલેક્ટ્રીક મુક્તા નવા કેપેસિટન્સ $'x'$ $pF$ હોય તો $'x'=.......$
JEE MAIN 2021, Diffcult
Download our app for free and get started
b
\(A =100 m ^{2}\)
\(A =100 m ^{2}\)
Using \(C =\frac{ k \in_{0} A }{ d }\)
\(C _{1}=\frac{10 \epsilon_{0}(100)}{5}\)
\(=200 \in_{0}\)
\(C _{2}=\frac{\epsilon_{0}(100)}{5}=20 \epsilon_{0}\)
\(C _{1} \& C _{2}\) are in series so \(C _{ eqv. }=\frac{ C _{1} C _{2}}{ C _{1}+ C _{2}}\)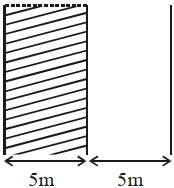
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
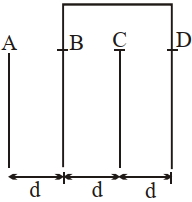
- 1$l=2\, cm$ લંબાઈ અને $b =\frac{3}{2}\, cm$ પહોળાઈ ધરાવતી ચાર સમાન લંબચોરસ પ્લેટને આકૃતિમાં દર્શાવ્યા મુજબ ગોઠવેલ છે. $A$ અને $C$ વચ્ચે સમતુલ્ય કેપેસીટન્સ $\frac{ x \varepsilon_{0}}{ d } $ હોય તો $x$નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું હશેView Solution
- 2બે સમાન ભારિત ગોળાઓ સમાન લંબાઈની દોરી વડે લટકાવેલા છે. દોરી એકબીજાથી $\theta$ કોણે છે. જ્યારે તેમને પાણીમાં લટકાવીએ, કોણ સમાન રહે છે. જો ગોળાના દ્રવ્યની ધનતા $1.5 \mathrm{~g} / \mathrm{cc}$ હોય તો પાણીનો ડાયઈલેક્ટ્રિક અચળાંક________હશે. ( પાણીની ઘનતા $=1 \mathrm{~g} / \mathrm{cc}$ લો.)View Solution
- 3$\vec p$ મોમેન્ટ ધરાવતી એક વિદ્યુત ડાઇપોલને વિદ્યુતક્ષેત્ર $\vec E$ ની દિશામાં મૂકેલો છે.આ ડાઇપોલને $90 ^o $ ના કોણે ભ્રમણ કરાવવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 4$R _1$ ત્રિજ્યાના અલગ કરેલા સંધારકની સંધારકતા $n$ ગણી વધી જાય છે જ્યારે તેને $R _2$ ત્રિજ્યા ધરાવતા અને પૃથ્વી સાથે જોડેલા $(grounded)$ સમકેન્દ્રીય ગોળામાં મૂકવામાં આવે છે. તેમની ત્રિજ્યાઆનો ગુણોત્તર $\left(\frac{R_2}{R_1}\right) \ldots$ થશે.View Solution
- 5એક સમાંતર પ્લેટ કેપેસીટર (સંધારક) ની પ્લેટોની વચ્ચેના વિસ્તારમાં સમાંગ વિધુતક્ષેત્ર $'\overrightarrow{\mathrm{E}}'$ પ્રવર્તે છે, જે પ્લેટો વચ્ચેનું અંતર $'d'$ અને દરેક પ્લેટનું ક્ષેત્રફળ $'A'$ હોય તો સંધારકમાં સંગ્રહિત ઊર્જા $......$ છે.$\left(\varepsilon_{0}=\right.$ શૂન્યાવકાશની પરમીટીવીટી$)$View Solution
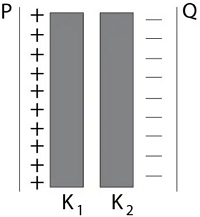
- 6આકૃતિમાં દર્શાવ્યા મુજબ એક સમાંતર પ્લેટ કેપેસિટરની પ્લેટો વચ્ચે $K_1$ અને $K_2 (K_2 > K_1)$ ડાઇઇલેકિટ્રક અચળાંકવાળા બે પાતળા ડાઇઇલેકિટ્રકોને મૂકવામાં આવેલ છે. કેપેસિટરની બે પ્લેટો વચ્ચેના વિદ્યુતક્ષેત્રનું મૂલ્ય $E$ પ્લેટ $P$ થી અંતર $d$ સાથેનો ફેરફાર કયો ગ્રાફ યોગ્ય રીતે રજૂ કરે છેView Solution
- 7$1\,m$ ત્રિજ્યા ધરાવતા વાહક ગોળાનું કેપેસીટન્સ કેટલું થાય?View Solution
- 8હવાનું આયનીકરણ થયા વગર મહત્તમ વિદ્યુતક્ષેત્ર $10^7\,V/m$ લગાવી શકાય છે. તો $0.10\,m$ ત્રિજયા ધરાવતા ગોળાને હવામાં મહતમ કેટલા વિદ્યુતસ્થિતિમાન સુધી ચાર્જ કરી શકાય?View Solution
- 9એક કેપેસીટરને ચાર્જ કરવા માટે એક બેટરી $200\,J$ જેટલું કાર્ય કરે છે. તેથી કેપેસીટરમાં સંગ્રહિત ઉર્જા $.......J$ હશે.View Solution
- 10$2 \times 10^{-2}\,C$ નો એક બિંદુવત વિદ્યુતભાર $P$ થી $S$ સુધી ધન $x-$ અક્ષની દિશામાં પ્રવર્તતા $30\,NC ^{-1}$ જેટલા નિયમિત વિદ્યુતક્ષેત્રમાં ગતિ કરે છે. જો $P$ અને $S$ના યામો અનુક્રમે $(1,2,0),(2,0,0),(1,-2,0)$ અને $(0,0,0)$ હોય, તો આ પ્રક્રિયામાં થતું કાર્ય $.........\,mJ$ થશે.View Solution