$12.5 \mathrm{pF}$ સંધારકતા ધરાવતા એક સમાંતર પ્લેટ કેપેસીટર (સંધારક)ને બે પ્લેટો વચ્ચે $12.0$ વોલ્ટના સ્થિતિમાનના તફાવત સાથે એક બેટરી થકી વિદ્યુતભારીત કરવામાં આવે છે. હવે બેટરીને દૂર કરવામાં આવે છે અને ડાયઇલેકટ્રીક યોસલા $\left(\epsilon_{\mathrm{r}}=6\right)$ ને પ્લટોની વચ્ચે સરકાવવામાં આવે છે. ડાયઇલેકટ્રીક ચોસલાને દાખલ કર્યા બાદ સ્થિતિઊર્જામાં ફેરફાર. . . . . . .$\times 10^{-12}$ $J$ હશે.
JEE MAIN 2024, Diffcult
c
Before inserting dielectric capacitance is given \(\mathrm{C}_0=12.5 \mathrm{pF}\) and charge on the capacitor \(\mathrm{Q}=\mathrm{C}_0 \mathrm{~V}\) After inserting dielectric capacitance will become \(\epsilon_{\mathrm{s}} \mathrm{C}_0\).
Before inserting dielectric capacitance is given \(\mathrm{C}_0=12.5 \mathrm{pF}\) and charge on the capacitor \(\mathrm{Q}=\mathrm{C}_0 \mathrm{~V}\) After inserting dielectric capacitance will become \(\epsilon_{\mathrm{s}} \mathrm{C}_0\).
Change in potential energy of the capacitor
\(=\mathrm{E}_{\mathrm{i}}-\mathrm{E}_{\mathrm{r}}\)
\(=\frac{\mathrm{Q}^2}{2 \mathrm{C}_{\mathrm{i}}}-\frac{\mathrm{Q}^2}{2 \mathrm{C}_{\mathrm{f}}}=\frac{\mathrm{Q}^2}{2 \mathrm{C}_0}\left[1-\frac{1}{\epsilon_{\mathrm{r}}}\right]\)
\(=\frac{\left(\mathrm{C}_0 \mathrm{~V}\right)^2}{2 \mathrm{C}_0}\left[1-\frac{1}{\epsilon_{\mathrm{r}}}\right]=\frac{1}{2} \mathrm{C}_0 \mathrm{~V}^2\left[1-\frac{1}{\epsilon_{\mathrm{r}}}\right]\)
Using \(\mathrm{C}_0=12.5 \mathrm{pF}, \mathrm{V}=12 \mathrm{~V}, \epsilon_{\mathrm{r}}=6\)
\(=\frac{1}{2}(12.5) \times 12^2\left[1-\frac{1}{6}\right]=\frac{1}{2}(12.5) \times 12^2 \times\)
\(\frac{5}{6}\)
\(=750 \mathrm{pJ}=750 \times 10^{-12} \mathrm{~J}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10\,\mu F$ ની સંઘારકતા ધરાવતા બે સમાંતર પ્લેટ સંઘારકો $C _1$ અને $C _2$ ને સ્વતંત્ર રીતે $100\,V\,D.C.$ ઉદગમથી વિદ્યુતભારિત કરવામાં આવે છે. સંઘારક $C _1$ ને ઉદગમ સાથે જોડેલા રાખીને તેની પ્લેટોની વચ્ચે અવાહક ચોસલું દાખલ કરવામાં આવે છે. સંઘારક $C _2$ એ ઉદગમથી છુટ્ટો કર્યા પછી તેની પ્લેટો વચ્ચે અવાહક ચોસલું દાખલ કરવામાં આવે છે. ત્યાર બાદ સંઘારક $C _1$ ને પણ ઉદગમથી છુટું કરી અંતમાં બંને સંઘારકોને સમાંતર જોડાણમાં જોડવામાં આવે છે. આ સંયોજનનું સામાન્ય સ્થિતિમાન $............\,V$ થશે.(ડાયઈલેક્ટ્રીક અચળાંક $=10$ છે તેમ ધારો)View Solution
- 2$200 \,\mu {F}$ ના સમાંતર પ્લેટ કેપેસીટરને $200 \, {V} $ ની બેટરી સાથે જોડેલ છે. બેટરીને જોડેલી રાખીને $2$ ડાઈઈલેક્ટ્રિક અચળાંક ધરાવતા ડાઈઈલેક્ટ્રિકને બે પ્લેટ વચ્ચે દાખલ કરવામાં આવે છે. કેપેસીટરની વિદ્યુતઊર્જામાં થતો ફેરફાર ($J$ માં) કેટલો હશે?View Solution
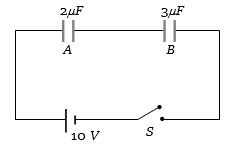
- 3કળ $S$ બંધ કરતાંView Solution
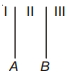
- 4આપેલ આકૃતિમાં વિદ્યુતભાર ધનતા $+\sigma$ અને $-\sigma$ ધરાવતી બે પ્લેટો અનુક્રમે $A$ અને $B$ દર્શાવેલ છે ક્યાં વિસ્તારમાં વિદ્યુત તીવ્રતા શૂન્ય હશે?View Solution
- 5આકૃતિમાં દર્શાવ્યા પ્રમાણે સાત એકસરખા ક્ષેત્રફળ $A$ ધરાવતી પ્લેટો $d$ જેટલા અંતરે રહેલી છે. આ સ્થિતિમાં બિંદુ $P$ અને $Q$ વચ્ચેનો અસરકારક કેપેસીટન્સ કેટલો થશે?View Solution

- 6$C_1$ કેપેસિટરને $V_0$ વોલ્ટેજથી ચાર્જ કરતાં તેની ઊર્જા $U_0$ છે.હવે,આ કેપેસિટર સાથે વિદ્યુતભાર રહિત કેપેસિટર $C_2$ સામંતરમાં જોડવાથી તે કેટલી ઉર્જા ગુમાવશે?View Solution
- 7View Solutionશા માટે કોઈ ધાતુનો કેપેસિટરમાં ડાઈ-ઈલેકટ્રીક તરીકે ઉપયોગ કરી શકાતો નથી ?
- 8બે $6\ pF$ વાળા કેપેસીટરોને શ્રેણીમાં જોડી જોડાણને સમાંતર $5000\, V$ આપવામાં આવે છે. હવે જોડાણને તોડીને તેમને સમાંતરમાં જોડવામાં આવે તો પ્લેટો વચ્ચેનું વિદ્યુતસ્થીતીમાન....View Solution
- 9$K$ જેટલો ડાઈઈલેક્ટ્રિક અચળાંક ધરાવતા ડાઈઈલેક્ટ્રીક ને એક $q$ જેટલો ચાર્જ ધરાવતા કેપેસીટરની બે પ્લેટો વચ્ચે દાખલ કરવામાં આવે છે. બે પ્લેટો વચ્ચે ઉત્પન્ન થયેલો પ્રેરિત ચાર્જ $q^{\prime}$ કયા સુત્રથી મળે?View Solution
- 10બે પ્લેટ વચ્યે હવા ધરાવતા સમાંતર પ્લેટ કેપેસીટરનું કેપેસીટન્સ $15\,pF$ છે. જો પ્લેટ વચ્યેનું અંતર બમણું કરવામાં આવે અને તમમાં $3.5$ ડાઈ ઈલેક્ટ્રીક અચળાંકનુ માધ્યમ દાખલ કરવામાં આવે તો કેપેસીટન્સનું મૂલ્ય $\frac{x}{4} pF$ થાય છે. તો $x$ નું મૂલ્ય $..........$ છે.View Solution
