\(I=\frac{1}{2} \varepsilon_{0} E_{0}^{2} C\) ..... \((i)\)
\(0.96\, \mathrm{I}=\frac{1}{2} \mathrm{E}_{0}^{2} \mathrm{V}\) ..... \((ii)\)
\(\Rightarrow \quad 0.96=\left(\frac{E_{0}^{\prime}}{E_{0}}\right)^{2} \frac{\varepsilon}{\varepsilon_{0}} \frac{V}{C}\)
\(0.96 = {\left( {\frac{{E_0^\prime }}{{{E_0}}}} \right)^2}\frac{\varepsilon }{{{\varepsilon _0}}}\frac{1}{{1.5}}\)
\({0.96=\left(\frac{E_{0}^{\prime}}{E_{0}}\right)^{2} \varepsilon_{r} \frac{1}{1.5}}\) ..... \((iii)\)
and \({\text{v}} = \frac{1}{{\sqrt {{\mu _{\text{o}}}{\varepsilon _{\text{o}}}{\mu _{\text{r}}}{\varepsilon _{\text{r}}}} }};\) \({\text{v}} = \frac{{\text{C}}}{{\sqrt {{\mu _{\text{r}}}{\varepsilon _{\text{r}}}} }}\)
\(\sqrt {{\mu _r}{\varepsilon _r}} = \frac{C}{v}\) ; \(\sqrt {{\varepsilon _r}} = 1.5\,;\) \({\mu _r} \approx 1\) for transparent medium.
From equation \((iii)\)
\(0.96=\left(\frac{E_{0}^{\prime}}{E_{0}}\right)^{2}(1.5)^{2}\left(\frac{1}{1.5}\right)\)
\(\Rightarrow E_{\circ}^{\prime}=24 \mathrm{V} / \mathrm{m}\)
Download our appand get started for free
Similar Questions
- 1સૂર્ય પરથી આવતા પ્રકાશમાં વિદ્યુતક્ષેત્રનું $ rms $ મૂલ્ય $720\, N\, C^{-1}$ છે. વિદ્યુતચુંબકીય તરંગોની સરેરાશ ઊર્જાઘનતા $= ...... J\, m^{-3} $View Solution
- 2View Solutionડિઝિટલ મૂવી પ્રોજેક્ટર ક્યા પ્રકાશનું પરાવર્તન
- 3View Solutionવિદ્યુતચુંબકીય તરંગોના અસ્તિત્વની સૌ પ્રથમ આગાહી ....... વૈજ્ઞાનિકે કરી.
- 4સમતલ વિદ્યુત ચુંબકીય તરંગોમાં વિદ્યુત ક્ષેત્ર સાઈન વક્રીય રીત $2 × 10^{10} \,Hz $ આવૃત્તિએ અને $48\, V/m $ કંપ વિસ્તાર પર દોલન કરે છે. તરંગની તરંગ લંબાઇ કેટલા ....$cm$ થશે?View Solution
- 5View Solutionકયો તરંગ લંબાઈના ચઢતા ક્રમ માટે સાયો વિકલ્પ છે;
- 6એક બિંદુવત ઉદગમસ્થાનમાંથી વિદ્યુતચુંબકીય તરંગો ઉત્સર્જાય છે. આ ઉદTગમસ્થાનનો આઉટપુટ પાવર $1500\, W$ છે, તો આ ઉદગમથી $3m$ દૂર આવેલા બિંદુએ વિદ્યુતક્ષેત્રનું મહત્તમ મૂલ્ય ........ $V \,M^{-1}$ હશે.View Solution
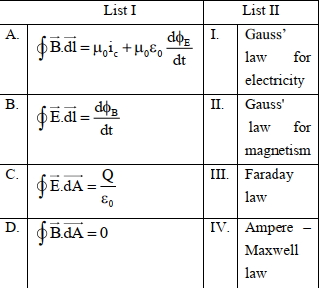
- 7સૂચિ $I$ સાથે સૂચિ $II$ને જોડો :View Solution
નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરોઃ
- 8એક ઉદ્ગમનો પાવર $4\;kW$ છે.તેમાંથી $10^{20}$ ફોટોન્સ $1$ $s$ માં ઉત્પન્ન થાય છે,તો આ ઉદ્ગમમાંથી ઉત્સર્જિત વિકિરણ વિદ્યુતચુંબકીય વર્ણપટમાંના કયાં વિકિરણો હશે?View Solution
- 9$E.M.$ તરંગ વર્ણ પટ્ટમાં $X -$ કિરણ પ્રદેશ ........ની વચ્ચે આવેલ છે.View Solution
- 10$3\, GHz$ આવૃત્તિ ધરાવતું એક વિદ્યુતચુંબકીય તરંગ શૂન્યાવકાશની સરખામણીમાં $2.25$ જેટલી પરમીટીવીટી (પારવિજાંક) ધરાવતાં અવાહક માધ્યમમાં દાખલ થાય છે. આ માધ્યમમાં તરંગની તરંગલંબાઈ $.......\,\times 10^{-2} \, cm$ થશે.View Solution
