$+ 1\,\mu C$ જેટલો વિજભાર ધરાવતો બિંદુવત વિજભાર $(0, 0, 0) $ પર છે. એક વિજભારરહિત વાહક ગોળાનું કેન્દ્ર $(4, 0, 0)$ આગળ છે. તો ગોળાના કેન્દ્ર આગળ વિદ્યુતસ્થિતિમાન અને વિદ્યુતક્ષેત્ર કેટલું મળે?
JEE MAIN 2013, Diffcult
c
\(\mathrm{q}=1\, \mu \mathrm{C}=1 \times 10^{-6} \,\mathrm{C}\)
\(\mathrm{q}=1\, \mu \mathrm{C}=1 \times 10^{-6} \,\mathrm{C}\)
\(r=4\, \mathrm{cm}=4 \times 10^{-2}\, \mathrm{m}\)
\( \text { Potential } V =\frac{\mathrm{k} q}{\mathrm{r}} \)
\(=\frac{9 \times 10^{9} \times 10^{-6}}{4 \times 10^{-2}} \)
\(=2.25 \times 10^{5}\, \mathrm{V} \)
Induced electric field \(\mathrm{E}=-\frac{\mathrm{kq}}{\mathrm{r}^{2}}\)
\(=\frac{9 \times 10^{9} \times 1 \times 10^{-6}}{16 \times 10^{-4}}=-5.625\, \times 10^{6}\, \mathrm{V} / \mathrm{m}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
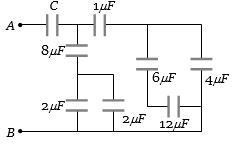
- 1$A$ અને $B$ વચ્ચે સમતુલ્ય કેપેસિટન્સ $1 \,\mu F$ છે.તો $C$ નું મૂલ્ય કેટલું હશે?View Solution
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે સાત એકસરખા ક્ષેત્રફળ $A$ ધરાવતી પ્લેટો $d$ જેટલા અંતરે રહેલી છે. આ સ્થિતિમાં બિંદુ $P$ અને $Q$ વચ્ચેનો અસરકારક કેપેસીટન્સ કેટલો થશે?View Solution

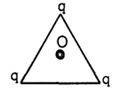
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે સમબાજુ ત્રિકોણના ત્રણેય ખૂણા પર ત્રણ સમાન વિદ્યુતભારો મૂકેલા છે. નીચના પૈકી (સામાન્ય નામકરણ) કેન્દ્ર આગળ $E$ અને $V$ માટે કયું વિધાન સાચું છે.View Solution
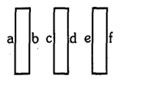
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે $A$ ક્ષેત્રફળ ધરાવતી દરેક ત્રણ સમાંતર ધાતુની પ્લેટો મુકેલી છે અને $Q_1$, $Q_2$ અને $Q_3$ વિદ્યુતભારો તેઓને આપવામાં આવે છે. છેડા (ધાર) પરની અસરો નગણ્ય છે. તો સૌથી બહારની બે સપાટીઓ $'a'$ અને $'f'$ પરનો વિદ્યુતભાર ગણો.View Solution
- 5પ્રોટોનનું દળ ઇલેક્ટ્રોન કરતાં $1840$ ગણું છે. $1\, kV$ વિદ્યુતસ્થિતિમાનથી પ્રવેગિત કરતાં ગતિઉર્જા ......$keV$ થાય.View Solution
- 6View Solutionવિદ્યુતભારીત કેપેસીટરની સંગ્રહીત ઊર્જા કયા સૂત્ર દ્વારા આપી શકાય ?
- 7એક બિંદુ $(x,y,z) $ આગળનું વિદ્યુતસ્થિતિમાન $V=-x^2y-xz^3 +4 $ છે.આ બિંદુ એ વિદ્યુતક્ષેત્રની તીવ્રતા _______View Solution
- 8સમબાજુ ત્રિકોણનાં શિરોબિંદુ પર $2 q,-q$ અને $-q$ મૂકવામાં આવે છે, ત્રિકોણનાં કેન્દ્ર પરView Solution
- 9બે $q$ વિજભાર ધરાવતા બિંદુવત કણને છત સાથે નહિવત દળ ધરાવતી સમાન લંબાઇની દોરી સાથે જોડેલા છે. તે જ્યારે સમતોલનમાં આવે ત્યારે દોરી શિરોલંબ સાથે $\theta$ ખૂણો બનાવે છે.જો દરેક વિજભારિત કણનું દળ $m$ હોય તો તે બંનેને જોડતી રેખા પર વિદ્યુતસ્થિતિમાન કેટલો મળે?View Solution
$\left( {\frac{1}{{4\pi { \in _0}}} = k} \right).$
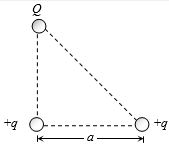
- 10સમદ્વિબાજુ કાટકોણ ત્રિકોણનાં શિરોબિંદુઓ પર $Q$, $+q$ અને $+q$ વિદ્યુતભારો આકૃતિ મુજબ મૂકેલ છે.જો સમગ્ર તંત્રની કુલ વિદ્યુતસ્થિતિઊર્જા શૂન્ય હોય,તો $Q$ = __________.View Solution