બે $q$ વિજભાર ધરાવતા બિંદુવત કણને છત સાથે નહિવત દળ ધરાવતી સમાન લંબાઇની દોરી સાથે જોડેલા છે. તે જ્યારે સમતોલનમાં આવે ત્યારે દોરી શિરોલંબ સાથે $\theta$ ખૂણો બનાવે છે.જો દરેક વિજભારિત કણનું દળ $m$ હોય તો તે બંનેને જોડતી રેખા પર વિદ્યુતસ્થિતિમાન કેટલો મળે?
$\left( {\frac{1}{{4\pi { \in _0}}} = k} \right).$
JEE MAIN 2013, Diffcult
c
In equilibrium, \(\mathrm{F}_{\mathrm{e}}=\mathrm{T} \sin \theta\)
In equilibrium, \(\mathrm{F}_{\mathrm{e}}=\mathrm{T} \sin \theta\)
\(\mathrm{mg}=\mathrm{T} \cos \theta\)
\(\tan \theta=\frac{F_{e}}{m g}=\frac{q^{2}}{4 \pi \epsilon_{0} x^{2} \times m g}\)
\(\therefore x = \sqrt {\frac{{{q^2}}}{{4\pi {\varepsilon _0}\,\tan \,\theta \,mg}}} \)
Electric potential at the centre of the line
\(V=\frac{k q}{x / 2}+\frac{k q}{x / 2}=4 \sqrt{k m g / \tan \theta}\)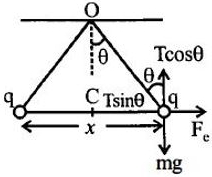
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમકેન્દ્રીય ત્રણ ગોળાકાર કવચની ત્રિજયાઓ $a,b$ અને $c\,\,(a < b < c)$ છે. આ ગોળા પરની વિદ્યુતભાર પૃષ્ઠઘનતા અનુક્રમે $\sigma ,-\;\sigma $ અને$\;\sigma \;$છે.જો $V_A,V_B$ અને $V_C$ એ કવચ પરનું વિદ્યુતસ્થિતિમાન દર્શાવતા હોય,તો $c=a+b$ માટે ____View Solution
- 2ધારો કે બે સંધારકોનાં (કેપેસીટરના) સંયોજન $C_1$ અને $C_2$ માટે $C_2 > C_1$ છે, જ્યારે તેમને સમાંતર જોડવામાં આવે છે ત્યારે તેમની સમતુલ્ય સંધારકતાં શ્રેણી જોડાણની સમતુલ્ય સંધારકતાં કરતાં $\frac{15}{4}$ ગણી છે. સંધારકોનો ગુણોત્તર $\frac{ C _{2}}{ C _{1}}$ ગણો.View Solution
- 3બે ગોળાકાર તકતીઓને $5$ $mm $ અંતરે રાખી તેમની વચ્ચે $2.2$ ડાયઇલેકિટ્રક અચળાંક ધરાવતો અવાહક મૂકો.એક સમાંતર પ્લેટ કેપેસિટરર્સ બનાવવામાં આવે છે.જયારે અવાહકનું વિદ્યુતક્ષેત્ર $3 \times 10^4$ $ Vm^{-1}$ હોય,ત્યારે ધન પ્લેટ (તકતી) ની વિદ્યુતભાર ઘનતા લગભગ _______ હશે.View Solution
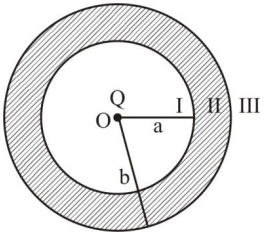
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે, આંતર ત્રિજ્યા $a$ અને બાહ્ય ત્રિજ્યા $b$ વાળા ગોળીય વાહક કવચના કેન્દ્રમાં બિંદુવત વીજભાર $Q$ મૂકેલ છે. વીજભાર $Q$ ને લીધે ત્રણ ભિન્ન વિસ્તાર $I, II$ અને $III$ માં વીજ ક્ષેત્ર $..............$ હશે. $\text { (I :r } r < a \text {, II : } a < r < b, \text { III: } r > b \text { ) }$View Solution
- 5નીચે બે વિધાનો આપેલા છે. એકને કથન $(A)$ અને બીભને કારણ $(R)$ થી દર્શાવામાં આવે છે.View Solution
કથન $(A)$: સમસ્થિતિમાન પૃષ્ઠ પરથી ધન વિદ્યુતભારને દૂર કરવા કરવું પડતું કાર્ય શૂન્ય હોય છે.
કારણ $(R)$: વિદ્યુત બળ રેખાઓ સમસ્થિતિમાન પૃષ્ઠે હંમેશા લંબ હોય છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં, નીચે આપેલા વિકલપોમાંથી સૌથી યોગ્ય ઉત્તર પસંદ કરો.
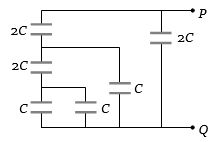
- 6View Solutionઆપેલ પરિપથનો સમતુલ્ય કેપેસીટન્સ કેટલો થાય?
- 7પારાના એકસમાન દરેક $512$ ટીપાંઓને $2\, V$ ના સ્થિતિમાનથી વીજભારિત કરવામાં આવે છે. ટીપાંઓને જોડીને એક ટીપું બનાવવામાં આવે છે. આ ટીપાનું સ્થિતિમાન .......... $V$ થશે.View Solution
- 8$C$ કેપેસીટન્સ ધરાવતા કેપેસીટરને $V$ વોલ્ટની બેટરી સાથે સમાંતરમાં જોડવામાં આવેલ છે હવે વિદ્યુતભાર સમાન રાખીને કેપેસીટરની બે પ્લેટો વચ્ચેનું અંતર અડધું કરવામાં આવે છે તથા ફરીથી તેને $V$ વોલ્ટ સુધી વિદ્યુતભારીત કરવામાં આવે તો બેટરી દ્વારા અપાતી ઉર્જા...?View Solution
- 9એક $8\; mC$ વિધુતભાર ઉગમબિંદુએ રહેલો છે. એક નાના $-2 \times 10^{-9} \;C$ વિધુતભારને $P (0,0,3\; cm )$ બિંદુથી $R (0,6\; cm , g \;cm )$ બિંદુએ થઈ $Q (0,4\; cm , 0),$ બિંદુએ લાવવા માટે કરેલું કાર્ય શોધો..View Solution
- 10વિદ્યુતસ્થિતિમાન $V = 4{x^2}\,volt$ છે.તો $(1m,\,0,\,2m)$ બિંદુ પર વિદ્યુતક્ષેત્ર કેટલું લાગે?View Solution
