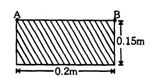
પિન \(B\) ને દૂર કરવામાં આવે તે સ્થતિ આકૃતિમાં દર્શાવેલી છે. ધારો કે લંબાઇ અને પહોળાઇ અનુક્રમે\(l\) અને \(b\) છે.
હવે પ્લેટ બિંદુ \(A\) ની આસ પાસ ભ્રમણની શરૂઆત કરે છે.
\(\tau \,\, = \,\,mg\,\,\left( {\frac{\ell }{2}} \right)\,\,\)
\(\Rightarrow \,\,\,I\alpha \,\, = \,\,mg\,\,\left( {\frac{\ell }{2}} \right)\,\,\,.......\,\,\,(i)\)
અહી,\(\,\, = \,\,0.2\,m,\,\,b\,\, = \,\,0.15\,m\,\, \Rightarrow \,\,\,{d^2}\, = \,\,\frac{{{\ell ^2}}}{4}\,\, + \,\,\,\frac{{{b^2}}}{4}\,\)
\( = \,\,\frac{{{{(0.2)}^2}}}{4}\,\, + \,\,\frac{{{{(0.15)}^2}}}{4}\,\, = \,\,\,\frac{{0.0625}}{4}\,\,{m^2}\)
\(A\) બિંદુ પર જડત્વની ચાકમાત્રા \(I = I_{CM} +Md^2\)
\(I\,\, = \,\,\frac{M}{{12}}\,\,\,({\ell ^2} + {b^2})\,\, + \,\,M{d^2}\,\)
\( = \,\,\frac{{20}}{{12}}\,[\,{(0.20)^2}\,\, + \,\,{(0.15)^2}]\,\, + \,\,20\,\, \times \,\,\,\frac{{0.0625}}{4}\,\,..........\,\,\,(ii)\)
સમી. (\(i\)) અને (\(ii\)) નો ઉકેલ શોધતાં \(\alpha = 48\ rad/s^2\)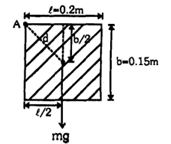
Download our appand get started for free
Similar Questions
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે એક દળરહિત $'a'$ બાજુવાળો સમબાજુ ત્રિકોણ $EFG$ ના શિરોબિંદુ પર ત્રણ $m$ દળના કણ મૂકેલા છે. ત્રિકોણ $EFG$ ના સમતલને અને બાજુ $EG$ ને લંબ બાજુ $EX$ રેખાને અનુલક્ષીને જડત્વની ચાકમાત્રા $\frac{ N }{20}\, ma ^{2}$ મળે છે. જ્યાં $N$ પૂર્ણાંક સંખ્યા છે. તો $N$ નું મૂલ્ય કેટલું હશે?View Solution
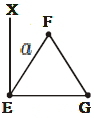
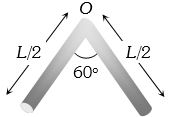
- 2$M$ દળ અને $L$ લંબાઇ ધરાવતા સળિયાને આકૃતિ મુજબ વાળવામાં આવે છે. $O$ માંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 3એક ટાવરની ટોચ પરથી $m$ દળ ના એક કણ ને સમક્ષિતિજ રીતે ફેક્વામાં આવે છે અને બીજી $2 \,m$ દળ ના ક્ણ ને ઊર્ધ્વ દિશામાં શિરોલંબ રીતે ફેકવામાં આવે છે તો દ્રવ્યમાન કેન્દ્રનો પ્રવેગ શું થાય?View Solution
- 4એક મીટર સ્ટીકનો તેનાં એક છેડો તળીયા પર રહે તેમ શિરોલંબ રીતે મૂકવામાં આવે છે અને તેને છોડવામાં આવે છે, જ્યારે તેનો બીજો છેડો તળીયા સાથે અથડાય ત્યારે તેની ઝડપ ............... $m / s$ (ધારો કે તળીયા પર રહેલો છેડો લપસી જતો નથી.) $\left(g=9.8 \,m / s ^2\right)$View Solution
- 5એક રીંગ અને ધન ગોળો સમાન ઢોળાવ પરથી સરક્યા સિવાય ગબડી રહ્યા છે. તેઓ વિરામસ્થિતિમાંથી શરૂ કરે છે. બંને પદાર્થોની ત્રિજ્યાં સમાન છે. તેઓની ગતિઉીર્જાઓનો ગુણોત્તર $\frac{7}{x}$ છે, જ્યાં $x$________થશે.View Solution
- 6View Solutionસમાન ત્રિજ્યાના એક નક્કર ગોળો અને તકતી ઢોળાવવાળી સપાટી પર લપસ્યા વગર પડે છે. એક એ બીજા કરતા વહેલા પહોંચે છે તેનું કારણ
- 7View Solutionસમાન ઊંચાઈ અને અલગ અલગ ખૂણો ધરાવતા ઢાળ પરથી ઘન ગોળાને ગબડાવતા બંને કિસ્સામાં ....
- 8નીચે આપેલા પદાર્થોને એક ઢાળ પર નીચેથી ઉપર તરફ (સરક્યાં વગર) ભ્રમણ કરવવામાં આવે છેView Solution
$(i)$ $R$ ત્રિજ્યાની રિંગ
$(ii)$ $\frac {R}{2}$ ત્રિજ્યાનો ઘન નળાકાર અને
$(iii)$ $\frac {R}{4}$ ત્રિજ્યાનો ઘન ગોળો
જો ઢાળના તળિયે બધાના દ્રવ્યમાન કેન્દ્રનો વેગ સમાન હોય તો તેમના દ્વારા પ્રાપ્ત થતી મહત્તમ ઊંચાઈનો ગુણોત્તર કેટલો થાય?
- 9$l$ લંબાઈના એક સળિયાના દ્રવ્યમાન કેન્દ્રથી $\frac{l}{4}$ અંતરે તેને લંબ અક્ષ માથી પસાર થતી અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા કેટલી થાય?View Solution
- 10એક પોલો ગોળો તેની સંમિત અક્ષને સમાંતર (અનુલક્ષીને) એક સમતલ સપાટી ઉપર ગબડે છે તેની ચાકગતિ ઉર્જા અને કુલ ગતિઉર્જાનો ગુણોતર $\frac{x}{5}$ છે. $x$ નું મૂલ્ય. . . . . . .હશે.View Solution
