$25\,W -220\,V$ અને $100\,W -220\,V$ નાં બે વિદ્યુત ગોળાઓ એક $440$ $ V$ નાં સપ્લાય સાથે શ્રેણીમાં જોડેલા છે ................ $W$ વિદ્યુત ગોળો ફયુઝ થશે?
AIEEE 2012, Diffcult
d
The current upto which bulb of marked \(25\,W - 220\,V,\) will
The current upto which bulb of marked \(25\,W - 220\,V,\) will
not fuse \(I_{1}=\frac{W_{1}}{V_{1}}=\frac{25}{220} \,\mathrm{Amp}\)
Similarly, \(\mathrm{I}_{2}=\frac{W_{2}}{V_{2}}=\frac{100}{220} \,\mathrm{Amp}\)
The current flowing through the circuit
\(I=\frac{440}{R_{e f f}}, \quad \mathrm{R}_{\mathrm{eff}}=R_{1}+R_{2}\)
\(R_{1}=\frac{V_{1}^{2}}{P_{1}}=\frac{(220)^{2}}{25} ; \quad R_{2}=\frac{V_{2}^{2}}{P}=\frac{(220)^{2}}{100}\)
\(I=\frac{440}{\frac{(220)^{2}}{25}+\frac{(220)^{2}}{100}}=\frac{440}{(220)^{2}\left[\frac{1}{25}+\frac{1}{100}\right]}\)
\(I=\frac{40}{220} \,\mathrm{Amp}\)
\({I_1}\left( { = \frac{{25}}{{220}}A} \right) < I\left( { = \frac{{40}}{{220}}A} \right) < {I_2}\left( { = \frac{{100}}{{200}}A} \right)\)
Thus the bulb marked \(25\, \mathrm{W}-220\) will fuse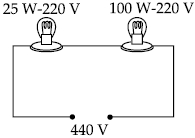
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1હિટરનો અવરોઘ $110\,Ω$ છે.તેને અવરોઘ $R$ સાથે સમાંતર જોડીને તંત્રને $11\,Ω$ અવરોઘ સાથે શ્નેણીમાં જોડવાનું છે.તેને $220\,V$ સાથે લગાવવામાં આવે છે.હિટરનો પાવર $110\,W$ છે તો $R$નું મૂલ્ય કેટલું થાય?View Solution
- 2મીટરબ્રીજમાં બે ગેપમાં અનુક્રમે $10\, \Omega$ અને $30 \,\Omega$ નાં અવરોધ છે. આ અવરોધોની અદલા બદલી કરતાં તટસ્થ બિંદુ.....સેમી ખસશે.View Solution
- 3જો તાંબાના તારને તેની લંબાઈમાં $20\%$ વધારો મેળવવા માટે ખેંચવામાં આવે તો તેના અવરોધમાં $.............\%$ વધારો થાય.View Solution
- 4સમાન $emf$ $E$ અને સમાન આંતરિક અવરોધ $r$ ઘરાવતાં એક હજાર કોષોને સમાન ક્રમમાં શ્રેણીમાં બાહ્ય અવરોધ વગર જોડાય છે. તો $399$ કોષો વચ્ચે થતો ......... $E$ છે.View Solution
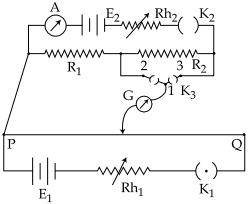
- 5આકૃતિમાં દર્શાવ્યા પ્રમાણે બે અવરોધની સરખામણી કરવા માટે પોટેન્શિયોમીટર $PQ$ વાપરવામાં આવે છે. જ્યારે કળ $K_3$ ખુલ્લી હોય ત્યારે $A$ એમીટર $1.0\, A$ નો પ્રવાહ દર્શાવે છે. જ્યારે કળ $K_3$ ને $2$ અને $1$ વચ્ચે જોડેલી હોય ત્યારે તટસ્થ બિંદુ $P$ થી $l_1\, cm$ અંતરે મળે છે, જ્યારે કળ $K_3$ ને $3$ અને $1$ વચ્ચે જોડેલી હોય ત્યારે તટસ્થ બિંદુ $P$ થી $l_2\, cm$ અંતરે મળે છે. તો બંન્ને અવરોધનો ગુણોત્તર $\frac{{{R_1}}}{{{R_2}}}$ કેટલો મળે?View Solution
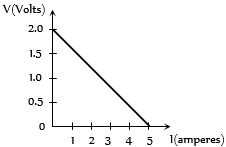
- 6બેટરીનો ટર્મિનલ વોલ્ટેજ અને પ્રવાહનો આલેખ આપેલ છે.તો $emf $ અને આંતરિક અવરોધ કેટલો થાય?View Solution
- 7$100 \,W, 220\, V $ ની કોઇલના બે ટુકડા કરી તેને સમાંતરમાં જોડતા $1 \,sec$ માં કેટલા ......... $J$ ઉષ્મા ઉત્પન્ન થાય?View Solution
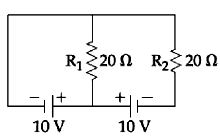
- 8આપેલ પરિપથમાં, વિદ્યુતકોષોને શૂન્ય આંતરિક અવરોધ છે. અવરોધો $R_1$ અને $R_2$ માંથી વહેતો પ્રવાહ (એમ્પિઅર માં), અનુક્રમે કેટલો હશે?View Solution
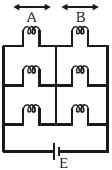
- 9શૂન્ય આંતરિક અવરોધના અને $E \;emf$ ના એક $DC$ ઉદગમ સાથે આકૃતિમાં બતાવ્યા પ્રમાણે છ સમાન બલ્બ જોડેલ છે. જ્યારે $(i)$ બધાજ બલ્બ ચાલુ હોય તેમાંથી $(ii)$ વિભાગ $- A$ ના બે અને વિભાગ $-B$ નો એક બલ્બ ચાલુ હોય તે પરિસ્થિતિઓમાં વપરાતાં પાવરનો ગુણોત્તર કેટલો હશે?View Solution
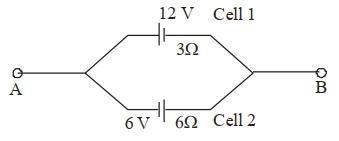
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે પરિપથમાં $A$ અને $B$ બિંદુઓ સાથે વીજકોષો જોડેલા છે. વીજ કોષ $1$ નું $emf \;12\,V$ અને આંતરિક અવરોધ $3\,\Omega$ છે. વીજકોષ $2$ નું $emf\,6\,V$ અને આંતરિક અવરોધ $6\,\Omega$ છે. $A$ અને $B$ સાથે $4\,\Omega$ નો બાહ્ય અવરોધ જોડેલો છે. તો $R$ માંથી વહેતો વીજ પ્રવાહ $.........A$ છે.View Solution