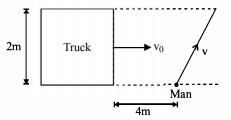
$2\,m$ પહોળાઈનો ટ્રક સીધા આડા રસ્તા પર $v _0=8\,m / s$ ના નિયમિત વેગથી ગતિ કરે છે. એક રાહધરી $v$ જેટલા નિયમિત વેગ થી રોડ ક્રોસ કરે છે જ્યારે ટ્રક તેનાથી $4\,m$ દૂર હોય છે. તે સુરક્ષિત રીતે રોડ ક્રોસ કરે તે માટે $v$ ની ન્યુનત કિંમત $...........\frac{m}{s}$

Diffcult
c
(c)
(c)
Let the man starts crossing the road at an angle \(\theta\) as shown in figure. For safe crossing the condition is that the man must cross the road by the time the truck describes the distance \(4+A C\) or \(4+2 \cot \theta\).
\(\therefore \frac{4+2 \cot \theta}{8}=\frac{2 / \sin \theta}{v}\)
or \(\quad v=\frac{8}{2 \sin \theta+\cos \theta}\)
For minimum \(v, \frac{d v}{d \theta}=0\)
or \(\frac{-8(2 \cos \theta-\sin \theta)}{(2 \sin \theta+\cos \theta)^2}=0\)
or \(2 \cos \theta-\sin \theta=0\)
or \(\tan \theta=2\)
From equation (i),
\(v_{\min }=\frac{8}{2\left(\frac{2}{\sqrt{5}}\right)+\frac{1}{\sqrt{5}}}=\frac{8}{\sqrt{5}}=3.57\,m / s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે ગોળાઓ $A$ અને $B$ ને $40\,m / s$ અને $60\,m / s$ ના શરૂઆતી વેગો સાથે સમક્ષિતિજની સાપેક્ષે $30^{\circ}$ અને $60^{\circ}$ ના ખૂણે ફેંકવામાં આવે છે. તેની સીમાઆનો ગુણોત્તર છે. $\left(g=10\,m / s ^2\right)$View Solution
- 2ચોક્કસ ગ્રહ (કોઈ વાતાવરણ વિના) પર જમીન પરથી ઉદ્ભવેલ પ્રક્ષેપણની સ્થાનનું નિર્દેશન $y=\left(4 t-2 t^2\right) m$ અને $x=(3 t) m$ દ્વારા આપવામાં આવે છે, જ્યાં $t$ સેકન્ડમાં છે અને પ્રક્ષેપણના બિંદુને ઉગમબિંદુ તરીકે લેવામાં આવે છે. શિરોલંબ સાથે પ્રક્ષિપ પદાર્થનો પ્રક્ષેપણ ખૂણો કેટલો હોય?View Solution
- 3View Solutionએક ટ્રેન ઉત્તર દિશામાં ગતિ કરે છે. એક જગ્યાએથી તે ઉત્તર-પૂર્વ દિશામાં વળાંક લે છે, તો એવું તારણ કાઢી શકાય કે....
- 4નિયમીત ઝડપે $R$ ત્રિજ્યાના વર્તુંળ પર ગતિ કરતો કણ એક પરિભ્રમણ પૂરું કરવા માટે $T$ સમય લે છે. જો આ કણને તેટલી જ ઝડપથી સમક્ષિતિજ થી $\theta$ કોણે પ્રક્ષિત્ કરવામાં આવે તો તેણે પ્રપ્ત્તિ કરેલી મહત્તમ ઉંચાઈ $4 \mathrm{R}$ છે. તો પ્રક્ષિપ્ત્ત કોણ $\theta$ બરાબર_________થાય.View Solution
- 5$\alpha= 30^o$ ખૂણો ધરાવતા ઢાળ પર સમક્ષિતિજ સાથે $\beta = 60^o$ ના ખૂણે $21 \,m/sec$ ના વેગથી ગોળી છોડતાં અવધિ ....... $m$ મળે .View Solution
- 6એક કણ $\left( {\frac{{20}}{\pi }} \right)\,m$ ત્રિજયાના વર્તુળાકાર પથ પર અચળ સ્પર્શીય પ્રવેગથી ગતિ કરે છે. જો ગતિની શરૂઆત પછી બે પરિભ્રમણના અંતે તેનો વેગ $80 \,m/s$ થાય ,તો સ્પર્શીય પ્રવેગ($m/s^2$) કેટલો હશે?View Solution
- 7એક દડાને $\theta$ ખૂણે સમક્ષિતિજ દિશામાં ફેકવામાં આવે છે. તેની સમક્ષિતિજ અવધિ તેની મહત્તમ ઊંચાઈ જેટલી છે.તો $\tan \theta$ ની કીમત કેટલી હશે?View Solution
- 8એક પૈડું અચળ કોણીય પ્રવેગથી ભ્રમણ કરે છે.શરૂઆતની કોણીય ઝડપ શૂન્ય છે.પ્રથમ $2 \,sec$ માં ${\theta _1}$ અને પછીની $2 \,sec$ માં ${\theta _2}$ કોણીય સ્થાનાંતર કરે છે.તો ${\theta _2}\over{\theta _1}$ = _____View Solution
- 9$100 \,m$ દૂર બંદુક દ્વારા નિશાનને અથડાવવા માટે ગોળીને ........ $cm$ ઊંચાઇ પરથી છોડવી જોઇએ. ગોળીનો સમક્ષિતિજ વેગ $500 \,ms^{-1}$ છે. $( g = 10 \,ms^{-2})$View Solution
- 10પૂર્વ સાથે $45^°$ ના ખૂણે $6\, km$ અંતર કાપ્યા પછી કાર પૂર્વ સાથે $135^°$ ના ખૂણે $4\, km$ અંતર કાપે છે, તો ઉદ્ગમબિંદુથી કેટલા અંતરે હશે?View Solution
