$30 \,cm$ અને $5 \,cm$ ત્રિજ્યાના બે સમકેન્દ્રી વાહક ગોલીય કવચ વિદ્યુતભારિત કર્યા છે. જો બાહ્ય કવચ પર $3\ \mu c$ અને આંતરિક કવચ પર $0.5\ \mu c$ વિદ્યુતભાર હોય તો બાહ્ય ગોલીય કવચ પરનું વિદ્યુત સ્થિતિમાન કેટલું થશે?
Medium
Download our app for free and get started
a
બાહ્ય ગોલીય કવચ પરનું વિદ્યુતસ્થિતિમાન
બાહ્ય ગોલીય કવચ પરનું વિદ્યુતસ્થિતિમાન
\(V = - \frac{{k{q_1}}}{R} + \frac{{k{q_2}}}{R}\,\,\,\,\therefore \,\,\,V = \frac{k}{R}({q_1} + {q_2})\,\)
\( = \frac{{9 \times {{10}^9}(3 \times {{10}^{ - 6}} + 0.5 \times {{10}^{ - 6}})}}{{30 \times {{10}^{ - 2}}}} = \frac{{9 \times {{10}^9} \times 3.5 \times {{10}^{ - 6}}}}{{30 \times {{10}^{ - 2}}}}\,V = 10.5 \times {10^4}\ V\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
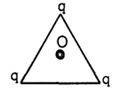
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે સમબાજુ ત્રિકોણના ત્રણેય ખૂણા પર ત્રણ સમાન વિદ્યુતભારો મૂકેલા છે. નીચના પૈકી (સામાન્ય નામકરણ) કેન્દ્ર આગળ $E$ અને $V$ માટે કયું વિધાન સાચું છે.View Solution
- 2એક નળાકાર કેપેસીટરની લંબાઈ $20\,cm$ છે અને તે $2 r$ અને $r$ જેટલી ત્રિજ્યાઓ ધરાવતા બે નળાકારોની વચ્ચે છે. નળાકાર પરનો વિદ્યુતભાર $-10 \mu C$ હોય તો બંને નળાકાર વચ્ચેનો સ્થિતિમાનનો તફાવત શોધો.View Solution
- 3એક સમાંતર પ્લેટ કેપેસિટર પાસે $20\, kV$ સ્થિતિમાન અને $2 \times 10^{-4}\ \mu F$ કેપેસિટન્સ છે. જો પ્લેટનું ક્ષેત્રફળ $0.01\, m^2$ હોય અને પ્લેટો વચ્ચેનું અંતર $2\ mm$ હોય તો સ્થિતિમાન પ્રચલન શોધો.View Solution
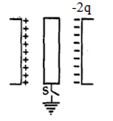
- 4આકૃતિમાં દર્શાવેલ ડાબી બાજુની ધાતુની પ્લેટ પર $+q$ વિદ્યુતભાર છે. જમણી બાજુની ધાતુની પ્લેટ $-2q$ વિદ્યુતભાર છે. પ્લેટથી પૃથ્વી તરફ કયો વિદ્યુતભાર વહન પામતો હશે ? જ્યારે $S$ બંધ છે જો મધ્યવર્તીં પ્લેટ પ્રારંભમાં તટસ્થ છે.View Solution
- 5નીચેના વિધાન $-1$ અને વિધાન $-2$ વાંચીને યોગ્ય વિકલ્પ પસંદ કરો.View Solution
વિધાન $-1$ : એક વિદ્યુતભારિત કણ $P$ થી $Q$ તરફ ગતિ કરે છે. આ દરમિયાન વિદ્યુતક્ષેત્ર દ્વારા કણ પર થતું કાર્ય એ $P$ થી $Q$ તરફના ગતિમાર્ગ પર આધારિત નથી.
વિધાન $-2$ : બંધ માર્ગમાં ગતિ કરતાં કણ પર સંરક્ષી બળ વડે થતું કાર્ય શૂન્ય હોય છે.
- 6એક સમાંતર પ્લેટ કેપેસિટર પાસે $400\, cm^2$ ક્ષેત્રફળ ધરાવતી લંબચોરસ પ્લેટો છે. અને હવાના માધ્યમ સાથે $2 \,mm $ ના અંતરેથી અલગ કરેલી છે. જો કેપેસિટરની વચ્ચે $200 \,volt$ સ્થિતિમાન તફાવત લગાડવામાં આવે તો પ્લેટો પરનો વિદ્યુતભાર કેટલો હશે?View Solution
- 7ધાતુના ગોળા દ્વારા ઉત્પન્ન થતાં વિદ્યુતક્ષેત્રમાં $4.5\, J$ ઉર્જાનો સંગ્રહ થાય છે. જો ગોળા પર $4\,\mu C$ વિજભાર હોય તો તેની ત્રિજ્યા $mm$માં કેટલી હશે? [$\frac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}\,N - {m^2}\,/{C^2}$]View Solution
- 8સમાન કેપેસિટન્સ $C$ ધરાવતાં કેપેસિટરને $V_1$ અને $V_2$ વોલ્ટેજથી ચાર્જ કરીને સમાંતરમાં જોડતાં તે કેટલી ઊર્જા ગુમાવશે?View Solution
- 9$10\, \mu F$ કેપેસીટન્સ ધરાવતું કેપેસીટર $50\, V$ ના વિદ્યુતસ્થિતિમાન વડે સંપૂર્ણ ચાર્જ કરેલ છે. હવે આ વિદ્યુતસ્થિતિમાનને દૂર કરી તેને બીજા વિજભારરહિત કેપેસીટર સાથે સમાંતરમાં જોડવામાં આવે છે. હવે તેમની વચ્ચેનો વિદ્યુતસ્થિતિમાનનો તફાવત $20\, V$ થાય છે, તો બીજા કેપેસીટરનો કેપેસીટન્સ ($\mu F$ માં) કેટલો હશે?View Solution
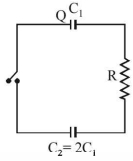
- 10આકૃતિમાં બતાવ્યા પ્રમાણે કેપેસિટરર $C _1$ અને $C _2=2 C _1$ ને તેમની વચ્ચે સ્વિય રહે તેમ પરિપથમાં જોંડલ છે. પ્રાંભમાં સ્વિચ ખુલ્લી છે અને વીજભાર $Q$ છે. $C _1$ પર સ્વીય બંધ છે. સ્થિર સ્થિતિમાં, દરેક કેપેસિટર પર વીજભાર $................$View Solution
