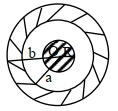
$+3\,Q$ વિદ્યુતભાર ધરાવતા ગોળાને $-Q$ વિદ્યુતભાર ધરાવતી ગાળીય કવચની અંદર સમકેન્દ્રિય મૂકેલ છે.ગોળાની ત્રિજયા $a$ એ ગોળીય કવચની ત્રિજયા $b(b>a)$ કરતાં નાની છે.હવે,કેન્દ્રથી $R>a$ બિંદુએ વિદ્યુતક્ષેત્ર કેટલું થાય?
Medium
Download our app for free and get started
c
(c) Electric field at a distance \(R\) is only due to sphere because electric field due to shell inside it is always zero. Hence electric field = \(\frac{1}{{4\pi {\varepsilon _0}}}.\frac{{3Q}}{{{R^2}}}\)
(c) Electric field at a distance \(R\) is only due to sphere because electric field due to shell inside it is always zero. Hence electric field = \(\frac{1}{{4\pi {\varepsilon _0}}}.\frac{{3Q}}{{{R^2}}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionવિદ્યુત બળ રેખાઓની દિશામાં તેના વેગ સાથે ઈલેકટ્રોન તેના વિદ્યુતક્ષેત્રમાં દાખલ થાય તો.......
- 2$+q$ અને $-q$ વિદ્યુતભાર ધરાવતા બે કણને અમુક અંતરે મૂકતાં તેમની વચ્ચે લાગતું બળ $F$ છે.બંને કણની વચ્ચે $+q$ વિદ્યુતભાર ધરાવતા કણ મૂકવાથી તેના પર કેટલું બળ લાગે?View Solution
- 3$Q$ વિદ્યુતભારને બે ભાગ $q$ અને $(Q-q)$ માં એવી રીતે વિભાજિત કરવામાં આવે છે કે જેથી $q$ અને $(Q-q)$ ને અમુક અંતરે મુક્તા તેમની વચ્ચે મહત્તમ સ્થિતવિદ્યુત અપાકર્ષણ બળ લાગે?View Solution
- 4સમકેન્દ્રિય ગોળીય કવચ $A$ અને $B $ ની ત્રિજયાઓ $r_A$ અને $r_B(r_B>r_A)$ છે.તેના પર વિદ્યુતભાર $Q_A$ અને $-Q_B(|Q_B|>|Q_A|)$ છે.તો વિદ્યુતક્ષેત્ર વિરુધ્ધ અંતરનો નો આલેખ કેવો થાય?View Solution
- 5વિદ્યુતભાર $q$ ને સમાન વિદ્યુતભાર ધરાવતા બે $Q$ વિદ્યુતભારને જોડતી રેખાની મધ્યમાં મૂકવામાં આવે છે. જો ત્રણ વિદ્યુતભારનું તંત્ર સમતોલનમાં રહે જો $q=$View Solution
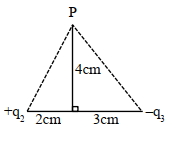
- 6આકૃત્તિમાં દર્શાવ્યા મુજબ, $Y$-અક્ષ પરના $P$ બિંદૂ ઓ પરિણામી વિદ્યુતક્ષેત્ર શૂન્ય હોય તો $\left|\frac{q_2}{q_3}\right|$ નો ગુણોત્તર $\frac{8}{5 \sqrt{x}}$ છે, જ્યાં $x=$. . . . . . .View Solution
- 7$\rho (r) = \frac{A}{{{r^2}}}{e^{ - 2r/a}}$ જ્યાં $A$ અને $a$ અચળાંકો છે, જેટલી કદ વિદ્યુતભાર ઘનતા ધરાવતા $R$ ત્રિજ્યાના ગોળામાં વિદ્યુત ભારનું વિતરણ થયેલ છે. જો $Q$ એ આ વિતરણનો કુલ વિધુતભાર હોય તો ત્રિજ્યા $R$ કેટલી હશે.View Solution
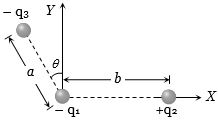
- 8ત્રણ વિદ્યુતભારો $ - {q_1},\,\, + {q_2}$ અને $ - {q_3}$ ને આકૃતિમાં બતાવ્યા પ્રમાણે મૂકવામાં આવ્યા છે. $- q_1$ વિદ્યુતભાર પર લાગતા બળનો $X$ ઘટક કોના સપ્રમાણમાં હોય?View Solution
- 9View Solutionવિદ્યુત ડાઈપોલની વિષુવ રેખા પરના એક બિંદુ માટે વિદ્યુતક્ષેત્રની તીવ્રતાની દિશા ....... છે.
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે અંદરની ત્રિજયા $a$ અને બહારની ત્રિજયા $b$ ધરાવતા ગોળીય કવચની અંદર $R$ ત્રિજયા અને $q$ વિદ્યુતભાર ધરાવતો ધાતુનો ગોળો છે. તો વિદ્યુતક્ષેત્ર $\overrightarrow{{E}}$ વિરુદ્ધ તેના કેન્દ્ર $O$ થી અંતર $r$ સાથેનો ગ્રાફ લગભગ કેવો મળશે?View Solution
