આકૃત્તિમાં દર્શાવ્યા મુજબ, $Y$-અક્ષ પરના $P$ બિંદૂ ઓ પરિણામી વિદ્યુતક્ષેત્ર શૂન્ય હોય તો $\left|\frac{q_2}{q_3}\right|$ નો ગુણોત્તર $\frac{8}{5 \sqrt{x}}$ છે, જ્યાં $x=$. . . . . . .
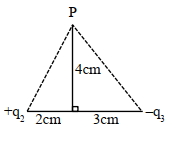

JEE MAIN 2024, Diffcult
c
\(\frac{\mathrm{Kq}_2}{20} \cos \beta=\frac{\mathrm{Kq}_3}{25} \cos \theta\)
\(\frac{\mathrm{Kq}_2}{20} \cos \beta=\frac{\mathrm{Kq}_3}{25} \cos \theta\)
\(\frac{\mathrm{Kq}_2}{20} \frac{4}{\sqrt{20}}=\frac{\mathrm{Kq}_3}{25} \frac{4}{\sqrt{25}}\)
\(\frac{\mathrm{q}_2}{\mathrm{q}_3}=\frac{20}{25} \sqrt{\frac{20}{25}}=\frac{8}{5 \sqrt{\mathrm{x}}}\)
\(\Rightarrow \sqrt{\mathrm{x}}=\frac{8 \times 25 \sqrt{25}}{5 \times 20 \sqrt{20}}\)
\(\mathrm{x}=5\)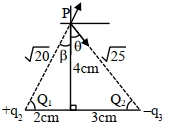
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
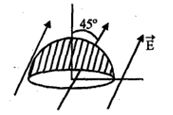
- 1સમક્ષિતિજ સમતલમાં તેની અંદરની બાજુની રેખા પર કોઈ વિદ્યુતભાર ન હોય તેવો $a$ ત્રિજ્યાનો સમતલ સપાટી વાળો એક અર્ધ ગોળો છે. તેની શિરોલંબ દિશા સાથે $\pi /4$ ખૂણો બનાવે તેમ સમાન વિદ્યુતક્ષેત્ર આવેલું છે. અર્ધ ગોળાની વક્ર સપાટીમાંથી પસાર થતું વિદ્યુત ફલક્સ ....... છે.View Solution
- 2બે પાતળી ધાતુની પ્લેટ પર સમાન અને વિરુધ્ધ સંજ્ઞા ધરાવતી વિજભાર ઘનતા $(\sigma = 26.4 \times 10^{-12}\,c/m^2)$ છે.બે પ્લેટ વચ્ચે વિદ્યુતક્ષેત્ર કેટલું હશે?View Solution
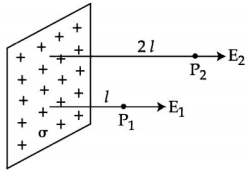
- 3આકૃતિમાં એક ખૂબ મોટું ધન વિદ્યુતભારિત સમતલ પૃષ્ઠ દર્શાવેલ છે. $P _{1}$ અને $P _{2}$ એ વિદ્યુતભાર વિતરણથી $l$ અને $2 l$ જેટલા લઘુત્તમ અંતરે બે બિંદુુઓ છે. જે પૃષ્ઠ વીજભાર ઘનતા $\sigma$ હોય, તો $P_{1}$ અને $P_{2}$ આગળ વિદ્યુતક્ષેત્ર $E_{1}$ અને $E_{2}$ માટે સાચો વિકલ્પ પસંદ કરોView Solution
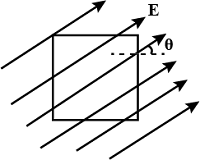
- 4આકૃતિમાં દર્શાવ્યા મુજબ $L$ મીટર બાજુવાળો એક ચોરસ સપાટીને પેપરના સમતલમાં ચોરસની સમક્ષિતિજ બાજુ સાથે $\theta$ ખૂણે $\vec E\;(V/m)$ જેટલા સમાન વિદ્યુતક્ષેત્રમાં મુકેલ છે, તો પૃષ્ઠ સાથે સંકળાયેલ ફલક્સ $volt \;m $ એકમમાં કેટલું થાય?View Solution
- 5$1$ $\mu$$C$ અને $5$ $\mu$$C$ ના બે વિદ્યુતભારો $4\, cm$ દૂર આવેલા છે. બંને વિદ્યુતભારો એકબીજા પર લાગતા બળનો ગુણોત્તર....... હશે.View Solution
- 6$9.1 \times {10^{ - 31}}\,kg$ દળ અને $1.6 \times {10^{ - 19}}\,coul.$ વિદ્યુતભાર પર $1 \times {10^6}\,V/m.$ વિદ્યુતક્ષેત્ર લગાવતાં તેનો વેગ પ્રકાશના વેગના $10$ માં ભાગનો થતાં કેટલો સમય લાગે?View Solution
- 7View Solutionહાઇડ્રોજન જેવા તંત્રમાં, ઇલેક્ટ્રોન અને પ્રોટોન વચ્ચેનાં કુલ્મબિય બળ અને ગુરુત્વકર્ષણ બળનો ગુણોત્તર . . . . .ના ક્રમનો હોય છે.
- 8ડ્યુટ્રોન અને $\alpha$ - કણ હવામાં એકબીજાથી $1\,\mathop A\limits^o $ અંતરે આવેલા છે. ડ્યુટ્રોનને લીધે $\alpha$ - કણ પર લાગતા વિદ્યુતક્ષેત્રનું મૂલ્ય ........ હશે.View Solution
- 9બે એકસમાન દરેક $Q$ એવા ધન વિદ્યુતભારોને એકબીજાથી $‘2a’$ જેટલા અંતરે દૂર મૂકવામાં આવ્યા છે. બીજા $m$ દળ ધરાવતો અને $q_0$ જેટલા એક બિંદુવત્ત વિદ્યુતભારને બે જડિત વિદ્યુતભારોની વચ્યે મૂકવામાં આવ્યા છે. બે વિદ્યુતભારોને જોડતી રેખા ઉપર $q_0$ વિદ્યુતભારનો આવર્તકાળ .......... હશે.View Solution
- 10સાચું વિધાન પસંદ કરો.View Solution
$(1)$ બળ રેખા પરના કોઈ પણ બિંદુ આગળ દોરેલો સ્પર્શક એ આપેલ બિંદુ આગળ ધન વિદ્યુતભાર પર લાગતા બળની દિશા આપે છે.
$(2)$ બળ રેખા પરના કોઈ પણ બિંદુ આગળ દોરેલ લંબ એ આપેલ બિંદુ આગળ ધન વિદ્યુતભાર પર લાગતા બળની દિશા આપે છે.
$(3)$ બળની વિદ્યુત રેખાઓ ઋણ વિદ્યુતભાર થી શરૂ કરીને ધન વિદ્યુતભાર પર પૂર્ણ થાય છે.
$(4)$ બળની વિદ્યુત રેખાઓ ધન વિદ્યુતભાર થી શરૂ કરીને ઋણ વિદ્યુતભાર પર પૂર્ણ થાય છે.
