$4.0\, cm$ અંતરે રહેલા, બે લાંબા સીધા અને સમાંતર તાર $A$ અને $B$ માંથી $8.0 \,A$ અને $5.0\, A$ વિદ્યુતપ્રવાહો એક જ (સમાન) દિશામાં વહે છે. તાર ના $10 \,cm$ લંબાઈના વિભાગ પર લાગતું બળ શોધો
Easy
d
Current flowing in wire \(A , I_{A}=8.0 \,A\)
Current flowing in wire \(A , I_{A}=8.0 \,A\)
Current flowing in wire \(B , I_{B}=5.0 \,A\)
Distance between the two wires, \(r=4.0 \,cm =0.04 \,m\)
Length of a section of wire A, \(l=10\, cm =0.1 \,m\)
Force exerted on length \(l\) due to the magnetic field is given as:
\(B=\frac{\mu_{0} 2 I_{A} I_{B} l}{4 \pi r}\)
Where,
\(\mu_{0}=\) Permeability of free space \(=4 \pi \times 10^{-7} \,T\,m\,A ^{-1}\)
\(B=\frac{4 \pi \times 10^{-7} \times 2 \times 8 \times 5 \times 0.1}{4 \pi \times 0.04}\)
\(=2 \times 10^{-5} \;N\)
The magnitude of force is \(2 \times 10^{-5}\,N\). This is an attractive force normal to A towards B because the direction of the currents in the wires is the same.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$i$ પ્રવાહધારિત લાંબા તારથી $r$ અંતરે ચુંબકીયક્ષેત્ર $0.4\, T$ છે. તારથી $2r$ અંતરે ચુંબકીયક્ષેત્ર ($Tesla$ માં) કેટલું થાય?View Solution
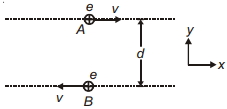
- 2બે પ્રોટોન $A$ અને $B, x$-અક્ષને સમાંતર, પરસ્પર વિરુદ્ધ દિશામાં, સમાન ઝડપે $V$ સાથે ગતિ કરે છે. દર્શાવેલ ક્ષણે, પ્રોટોન $A$ પર લાગતા ચુંબકીય બળ અને વિદ્યુતબળનો ગુણોત્તર કેટલો છે ? ($c =$ શૂન્યાવકાશમાં પ્રકાશની ઝડ૫)View Solution
- 3ન્યુક્લિયસને ફરતે ભમણ કરતા અને $L$ જેટલું કોણીય વેગમાન ધરાવતા ઇલેક્ટ્રોન $(e)$ ની ચુંબકીય ચાકમાત્રા $...............$ વડે આપી શકાય છે.View Solution
- 4બે ખૂબ લાંબા, સીધા, સમાંતર વાહક $A$ અને $B$ અનુક્રમે $5\,A$ અને $10\,A$ ના પ્રવાહનું વહન કરે છે અને તે એકબીજાથી $10\,cm$ ના અંતરે છે. બે વાહકમાં પ્રવાહની દિશા સમાન છે. બે વાહક વચ્ચે એકમ લંબાઈ દીઠ લાગતું બળ કેટલું હશે?$\left(\mu_0=4 \pi \times 10^{-7}\right. \;SI $ એકમમાં)View Solution
- 5$800\, mV$ ની રેન્જ અને $40 \,\Omega$ અવરોધ ધરાવતા વોલ્ટમીટરને $100\, mA$ રેન્જ ધરાવતા ગેલ્વેનોમીટરમાં ફેરવવા માટે તેની સાથે કેટલા $\Omega $ નો શંટ અવરોધ જોડાવો પડે?View Solution
- 6$1.5 \,m$ લંબાઇ અને $10 \,A$ પ્રવાહધારિત તારને $2T$ ચુંબકીયક્ષેત્રમાં મૂકતાં $15\, N$ બળ લાગે છે,તો ચુંબકીયક્ષેત્ર અને પ્રવાહની દિશા વચ્ચેનો ખૂણો કેટલા ......$^o$ થાય?View Solution
- 7$3\, cm$ ત્રિજયા ધરાવતી પ્રવાહધારિત રીંગની અક્ષ પર $4\, cm$ અંતરે ચુંબકીયક્ષેત્ર $54 \,\mu T$ છે,તો કેન્દ્ર પર ચુંબકીયક્ષેત્ર કેટલા ......$\mu T$ થાય?View Solution
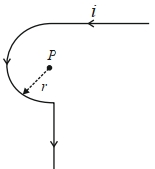
- 8આકૃતિમાં $P$ બિંદુ પર ચુંબકીય ક્ષેત્ર મેળવો. વક્ર ભાગ બે લાંબા સીધા તાર સાથે જોડાયેલ અર્ધવર્તુળ છે.View Solution
- 9$100$ આંટા અને $1 \,cm^2 $ ક્ષેત્રફળ ધરાવતા ગેલ્વેનોમીટરના કોઇલનો વળઅચળાંક $10^{-8 }\, N-m\, rad.$ છે.જો ચુંબકીયક્ષેત્ર $5 \,T$ હોય,તો પ્રવાહસંવેદીતા કેટલી થાય?View Solution
- 10એક લાંબા સીધા તારમાંથી $35\; A$ વિદ્યુતપ્રવાહ વહે છે. તારથી $20\; cm$ અંતરે રહેલા કોઈ બિંદુ પાસે ચુંબકીય ક્ષેત્ર $B$ નું મૂલ્ય કેટલું હશે?View Solution
