$40 \%$ કાર્યક્ષમતા ધરાવતા કાર્નોટ એન્જિન માટે ઠારણ વ્યવસ્થાનું તાપમાન $300\; K$ છે. તેની ઠારણ વ્યવસ્થાનું તાપમાન અચળ રાખીને,કાર્યક્ષમતા કરતાં $50 \% $ વધારવા માટે પ્રાપ્તિસ્થાનનું તાપમાન ..... $K$ વધારવું પડે.
AIPMT 2006, Diffcult
Download our app for free and get started
d
Efficiency of a Carnot engine,\(\eta = 1\frac{{{T_2}}}{{{T_1}}}\)
Efficiency of a Carnot engine,\(\eta = 1\frac{{{T_2}}}{{{T_1}}}\)
\(or,\,\,\frac{{{T_2}}}{{{T_1}}} = 1 - \eta = 1 - \frac{{40}}{{100}} = \frac{3}{5}\)
\(\therefore {T_1} = \frac{5}{3} \times {T_2} = \frac{5}{3} \times 300 = 500\,K.\)
\(Increases\,in\,efficiency = 50\% \,of\,40\% = 20\% \)
\(New\,efficiency,\eta ' = 40\% + 20\% = 60\% \)
\(\therefore \,\,\frac{{{T_2}}}{{{T_1}'}} = 1 - \frac{{60}}{{100}} = \frac{2}{5}\)
\({T_1}' = \frac{5}{2} \times {T_2} = \frac{5}{2} \times 300 = 750\,K.\)
\(Increases\,in\,temperature\,of\,source = {T_1}' - {T_1}\)
\( = 750 - 500 = 250\,K.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વાયુનો નમૂનો $V_1$ કદથી $V_2$ કદમાં વિસ્તરે છે. વાયુ દ્વારા થતું કાર્ય મહતમ હોય જ્યારે વિસ્તરણ .......... હોય.View Solution
- 2View Solutionદ્વિ પારિમાણ્યિક વાયુને ઉષ્મા આપતા તે અચળ દબાણે વિસ્તરણ થાય છે.ઉષ્માનો કેટલામો ભાગ આંતરિક ઊર્જામાં રૂપાંતર થયો હશે?
- 3એક રેફ્રિજરેટરનું અંદરનું તાપમાન $t_2\, ^o C$ છે અને ઓરડાનું તાપમાન $t_1 \,^o C$ છે. આદર્શ અવસ્થામાં પ્રતિજૂલ વિદ્યુતઊર્જાનો વ્યય થાય ત્યારે, ઓરડાને આપેલી ઉષ્માનું મૂલ્ય કેટલું હશે?View Solution
- 4કાર્નોટ એન્જિન પહેલા $200^{\circ}\,C$ અને $0^{\circ}\,C$ વચ્ચે કાર્ય કરે છે અને પછી $0^{\circ}\,C$ અને $-200^{\circ}\,C$ વચ્ચે કાર્ય કરે છે. બંને કિસ્સામાં તેમની કાર્યક્ષમતાનો ગુણોત્તર $...............$View Solution
- 5View Solutionસમકદ પ્રક્રિયા માટે નીચેનામાથી શું સાચું છે?
- 6વાયુનું શરૂઆતનું દબાણ અને કદ $ P$ અને $V$ છે.સમતાપી વિસ્તરણ કરીને કદ $ 4V$ અને સમોષ્મી સંકોચન કરીને કદ $V$ કરતાં અંતિમ દબાણ કેટલું થશે?$ [\,\,\gamma \, = \,1.5] $View Solution
- 7$18^oC$ રહેલા તાપમાને દ્વિ પરમાણ્વિક વાયુનું સમોષ્મી સંકોચન કરતાં કદ મૂળથી આઠમાં ભાગનું થાય છે. સંકોચન પછી તાપમાન કેટલું થાય?View Solution
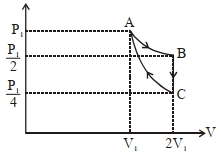
- 8$\left( P _{1}, V _{1}\right)$ એ રહેલ એક મોલ આદર્શ વાયુનું પ્રતિવર્તીય અને સમતાપીય વિસ્તરણ $(A$ થી $B)$ કરાવવામાં આવે, ત્યારે તેનું દબાણ મૂળ દબાણ કરતાં અડધું થાય છે. (આકૃતિ જુઓ) ત્યારબાદ તેનું અચળ કદે ત્યાં સુધી ઠારણ કરવામાં આવે છે કે જેથી તેનું દબાણ મૂળ દબાણ કરતાં ચોથા ભાગનું થાય $( B \rightarrow C )$ ત્યારબાદ પ્રતિવર્તી સમોષ્મી દબાણ દ્વારા $(C$ થી $A)$તેની મૂળ સ્થિતિ પ્રાપ્ત કરવામાં આવે છે. વાયુ દ્વારા થતું ચોખ્ખું કાર્ય ..... છે.View Solution
- 9એકમ દળના $ {V_1} $ કદના પ્રવાહીને $ {V_2} $ કદના વાયુમાં અચળ દબાણ $P $ અને તાપમાન $T$ એ રૂપાંતર કરવામાં આવે છે.બાષ્પાયનગુપ્ત ઉષ્મા $L$ હોય,તો તંત્રની આંતરિક ઊર્જામાં કેટલો વધારો થાય?View Solution
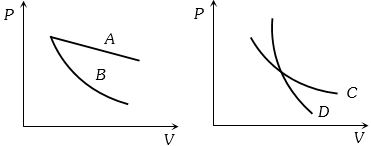
- 10વક્ર $A,B,C$ અને $D$ માટે નીચેનામાથી શું સાચું છે?View Solution
