\( \left|\overrightarrow{\mathrm{a}}_{\mathrm{c}}\right|=\left|\overrightarrow{\mathrm{a}}_{\mathrm{t}}\right| \)
\( \frac{\mathrm{v}^2}{\mathrm{r}}=\frac{\mathrm{dv}}{\mathrm{dt}} \)
\( \Rightarrow \int_4^{\mathrm{v}} \frac{\mathrm{dv}}{\mathrm{v}^2}=\int_0^{\mathrm{t}} \frac{\mathrm{dt}}{\mathrm{r}} \)
\( \Rightarrow\left[\frac{-1}{\mathrm{v}}\right]_4^{\mathrm{v}}=\frac{\mathrm{t}}{\mathrm{r}} \)
\( \Rightarrow \frac{-1}{\mathrm{v}}+\frac{1}{4}=2 \mathrm{t}\)
\( \Rightarrow \mathrm{v}=\frac{4}{1-8 \mathrm{t}}=\frac{\mathrm{ds}}{\mathrm{dt}} \)
\( 4 \int_0^{\mathrm{t}} \frac{\mathrm{dt}}{1-8 \mathrm{t}}=\int_0^5 \mathrm{ds} \)
\( (\mathrm{r}=0.5 \mathrm{~m} \)
\( \mathrm{s}=2 \pi \mathrm{r}=\pi) \)
\( 4 \times \frac{[\ln (1-8 \mathrm{t})]_0^{\mathrm{t}}}{-8}=\pi \)
\( \ln (1-8 \mathrm{t})=-2 \pi \)
\( 1-8 \mathrm{t}=\mathrm{e}^{-2 \pi} \)
\( \mathrm{t}=\left(1-\mathrm{e}^{-2 \pi}\right) \frac{1}{8} \mathrm{~s}\)
So, \(\alpha=8\)
Download our appand get started for free
Similar Questions
- 1ગતિ કરતાં કણના યામો $t$ સમયે $ x = \alpha t^3$ અને $y = \beta t^3$ વડે આપી શકાય છે,તો $t$ સમયે કણની ઝડપ કેટલી થાય?View Solution
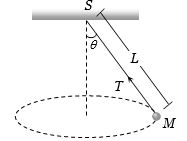
- 2આકૃતિમાં $M$ દળનો પદાર્થ $2/\pi $ પરિભ્રમણ$/sec$ ની કોણીય ઝડપથી ભ્રમણ કરે છે,તો દોરીમાં કેટલો તણાવ ઉત્પન્ન થશે?View Solution
- 3ગતિ કરતાં કણના યામો $t$ સમયે $ x = \alpha t^3$ અને $y = \beta t^3$ વડે આપી શકાય છે,તો $t$ સમયે કણની ઝડપ કેટલી થાય?View Solution
- 4એક કણનો પ્રારંભિક વેગ $(2\hat i + 3\hat j$ ) અને પ્રવેગ $(0.3\hat i + 0.2\hat j$ ) છે. તે કણની $ 10 \;s$ પછી ઝડપ કેટલી હશે?View Solution
- 5ચાર વ્યક્તિઓ $K,\,L,\,M$ અને $N$ એ $d$ ધીમે ધીમે ઘટતી બાજુ લંબાઈ વાળા ચોરસ ના ખૂણાઓ પર છે. $K$ એ $L$ તરફ, $L$ એ $M$ તરફ, $M$ એ $N$ તરફ અને $N$ એ $K$ તરફ ગતિ ચાલુ કરે , તો ચારેય વ્યક્તિઓ ક્યારે ભેગા થશે?View Solution
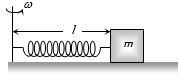
- 6$k$ બળઅચળાંક અને $l$ લંબાઇ ઘરાવતી સ્પ્રિંગના છેડે $m$ દળનો પદાર્થ બાંઘીને સમક્ષિતિજ સમતલમાં $\omega $ કોણીય ઝડપથી ફેરવતા સ્પ્રિંગની લંબાઇમાં કેટલો વધારો થાય?View Solution
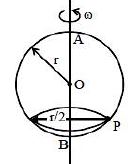
- 7એક $2\pi r$ લંબાઈના તારને વાળીને એક વર્તુળ બનાવીને શિરોલંબ સમતલમાં મૂકવામાં આવે છે એક મણકો તાર પર સરળતાથી સરકી શકે છે જ્યારે વર્તુળને આકૃતિમાં દર્શાવ્યા મુજબ $AB$ની સાપેક્ષે $\omega$ જેટલી કોણીય ઝડપથી ફેરવતા મણકો વર્તુળની સાપેક્ષે $P$ બિંદુ પાસે સ્થિર થાય છે તો $\omega^2$ નું મૂલ્ય કેટલું હશે?View Solution
- 8$M$ અને $m$ દળ ધરાવતા બે કણો અનુક્રમે $R$ અને $r$ ત્રિજ્યાના વર્તુળાકાર પથ પર ગતિ કરે છે. જો તેમનો આવર્તકાળ સમાન હોય, તો તેમના કોણીય વેગનો ગુણોત્તર કેટલો થાય?View Solution
- 9$R ^{3}$ નાં વ્યસ્ત પ્રમાણમાં ચલિત કેન્દ્રીય આભાસી બળ $F$ ની અસર હેઠળ એક કણ અચળ ઝડપથી $R$ ત્રિજ્યા ધરાવતાં વર્તુળનાં પરીઘ પર ગતિ કરે છે. તેનાં પરિભ્રમણનો આવર્તકાળ ......... દ્વારા દર્શાવવામાં આવે છે.View Solution
- 10એક પ્રક્ષિપ્ત પદાર્થની અવધિ $500\, m$ અને ઉડ્ડયન સમય $10 \,sec$ છે,તો પદાર્થે પ્રાપ્ત કરેલી ઊંચાઇ ......... $m$View Solution
