The given system of two masses and a pulley can be represented as shown in the following figure:
Smaller mass, \(m_{1}=8 \,kg\)
Larger mass, \(m_{2}=12\, kg\)
Tension in the string \(=T\)
Mass \(m_{2},\) owing to its weight, moves downward with acceleration \(a,\) and mass \(m_{1}\) moves upward.
Applying Newton's second law of motion to the system of each mass:
For mass \(m_{\underline{1}}:\) The equation of motion can be written as:
\(T-m_{1} g =m a\)
For mass \(m_{2}\) : The equation of motion can be written as:
\(m_{2} g -T=m_{2} a\)
Adding above equations , we get:
\(\left(m_{2}-m_{1}\right) g =\left(m_{1}+m_{2}\right) a\)
\(\therefore a=\left(\frac{m_{2}-m_{1}}{m_{1}+m_{2}}\right) g\)
\(=\left(\frac{12-8}{12+8}\right) \times 10=\frac{4}{20} \times 10=2 m / s ^{2}\)
Therefore, the acceleration of the masses is \(2 \;m / s ^{2}\)
Substituting the value of \(a\) in equation ( \(i i\) ), we get:
\(m_{2} g -T=m_{2}\left(\frac{m_{2}-m_{1}}{m_{1}+m_{2}}\right) g\)
\(T=\left(m_{2}-\frac{m_{2}^{2}-m_{1} m_{2}}{m_{1}+m_{2}}\right) g\)
\(=\left(\frac{2 m_{1} m_{2}}{m_{1}+m_{2}}\right) g\)
\(=\left(\frac{2 \times 12 \times 8}{12+8}\right) \times 10\)
\(=\frac{2 \times 12 \times 8}{20} \times 10=96\, N\)
Therefore, the tension in the string is \(96\, N\).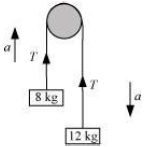
Download our appand get started for free
Similar Questions
- 1એક ગતિ કરતાં માલવાહક પટ્ટા પર $M\ kg/s $ ના દરથી રેતી પાડવામાં આવે છે. જો પટ્ટાનો અચળ વેગ $v\ m/s $ જાળવી રાખવો હોય,તો પટ્ટા પર કેટલું બળ લગાડવું જરૂરી છે?View Solution
- 2એક માણસ સ્પ્રિંગ પ્લેટફોર્મ પર ઊભો છે. તો સ્પ્રિંગકાંટા નું અવલોકન $60\, kg$ છે. જો તે માણસ પ્લેટફોર્મ પરથી બહાર તરફ કૂદે તો સ્પ્રિંગકાંટા નું અવલોકન ....View Solution
- 3$ m_1 = 4m_2$ છે . $m_2$ ને સ્થિર થવા માટે ........ $cm$ વધારાનું અંતર કાંપવું પડે.View Solution
- 4$50 \,g$ દળનાં એેક દડાને $20\,m$ ની ઉંચાઈથી ફેકવામાં આવે છે. એક જમીન પર ઉભેલો છોકરો $200 \,N$ નાં સરેરાશ બળ સાથે બેટથી દડાને શિરોલંબ રીતે ઉપર તરફ મારે છે. જેથી તે $45 \,m$ ની શિરોલંબ ઉંચાઈને પ્રાપ્ત કરે છે. તો દડાનો બેટ સાથેનો સંપર્ક સાથે રહેવાનો સમય શોધો.View Solution
[ $g=10 \,m / s ^2$ લો]
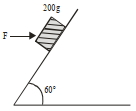
- 5$200 \,g$ દળ ધરાવતા ચોસલાને લીસા ઢોળાવ પર યોકકસ બળ $F$ દ્વારા સ્થિર ટેકવવામાં આવેલ છે. (આકૃતિ જુઓ) જો $F$ નું લધુત્તમ બળ મૂલ્ય $\sqrt{x} N$ હોય તો $x=$.......... થશે.View Solution
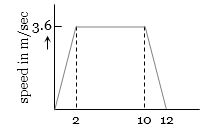
- 6$1500 \,kg$ દળ ધરાવતી લિફ્ટ ઉપર તરફ ગતિ કરતાં તેની ઝડપ વિરુધ્ધ સમયનો આલેખ આપેલ છે.તો $t= 11^{th}\,Sec$ સમયે કેબલમાં તણાવબળ ............ $N$ હશે.View Solution
- 7એક કણનો વેગમાન $p\left( kg m / s\right)$ માં એ સમય $t$ ($s$ માં) સાથે $p=2+3 t^2$ મુજબ બદલાય છે. તો $t=3 s$ એ કણ પર લગાડવામાં આવતું બળ ........... $N$ હશે.View Solution
- 8આકૃતિમાં દર્શાવેલ $30 \,cm$ લાંબા નિયમિત સળિયાનો દળ $3.0 \,kg$ છે. આ સળિયાને $20 \,N$ અને $32 \,N$ નાં અચળ બળો દ્વારા ખેંચવામાં આવે છે. સળિયાના $10 \, cm$ ભાગ પર $20 \,cm$ ભાગ દ્વારા લગાડેલું બળ ...............$N$. (તમામ સપાટી લીસી છે)View Solution
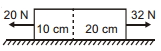
- 9View Solutionન્યૂટનનાં ગતિના ત્રીજા નિયમ મુજબ
- 10સમક્ષિતિજ ગતિ કરતા ખોખાની અંદર, અવલોકનકાર જોવે છે કે એક પદાર્થને સૂવાળા આડા ટેબલ પર મૂકીને છોડવામાં આવે તો તે $10\,m / s ^2$ ના પ્રવેગથી ગતિ કરે છે. જો આ ખોખામાં $1\,kg$ પદાર્થ હલકી દોરી દ્વારા લટકાવવામાં આવે, તો સંતુલન અવસ્થામાં દોરીમાં તણાવ (અવલોકનકારની દષ્ટિએ) $g =10\,m / s ^2 \ldots \ldots \ldots \ldots\,N$View Solution
