$8\,\mu F,\;250\, V$ ના કેપેસિટરથી $16\,\mu F,\;1000\, V$ નું કેપેસિટર બનાવવા માટે કેટલા કેપેસિટરની જરૂર પડશે?
AIIMS 2000, Diffcult
b
(b) Suppose \(C = 8\, µF ,\, C' = 16\,µF\)
and \(V = 250\, V,\, V' = 1000\,V\)
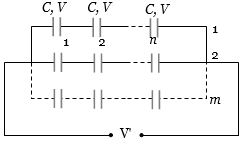
Suppose \(m\) rows of given capacitors are connected in parallel and each row contains \(n\) capacitors then potential difference across each capacitor \(V = \frac{{V'}}{n}\) and equivalent capacitance of network \(C' = \frac{{mC}}{n}\) on putting the values we get \(n = 4\) and \(m = 8\)
Total capacitors \(= n × m = 4 × 8 = 32\)
Short Trick : For such type of problems number of capacitors = \(\frac{{C'}}{C} \times {\left( {\frac{{V'}}{V}} \right)^2} = \frac{{16}}{8}{\left( {\frac{{1000}}{{250}}} \right)^2} = 32\)
(b) Suppose \(C = 8\, µF ,\, C' = 16\,µF\)
and \(V = 250\, V,\, V' = 1000\,V\)
Suppose \(m\) rows of given capacitors are connected in parallel and each row contains \(n\) capacitors then potential difference across each capacitor \(V = \frac{{V'}}{n}\) and equivalent capacitance of network \(C' = \frac{{mC}}{n}\) on putting the values we get \(n = 4\) and \(m = 8\)
Total capacitors \(= n × m = 4 × 8 = 32\)
Short Trick : For such type of problems number of capacitors = \(\frac{{C'}}{C} \times {\left( {\frac{{V'}}{V}} \right)^2} = \frac{{16}}{8}{\left( {\frac{{1000}}{{250}}} \right)^2} = 32\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$5\,mm$ બે પ્લેટ વચ્ચેનું અંતર ધરાવતા સમાંતર પ્લેટ કેપેસીટરનું કેપેસીટન્સ $3\,F$ હોય તો પ્લેટનું ક્ષેત્રફળ મેળવોView Solution
- 2$X$-અક્ષ પર વિદ્યુતભાર $Q$ અનુક્રમે $x = 1, 2, 4, 8…meter$ પર મૂકેલા છે,તો $x = 0$ પર વિદ્યુતક્ષેત્ર અને વિદ્યુતસ્થિતિમાન કેટલું થાય?View Solution
- 3જો $V\,\, = \,\, - 5x\,\, + \,\,3y\,\, + \,\,\sqrt {15} \,z\,$ હોય તો ${\text{E(x, y, z) = }}.....unit$View Solution
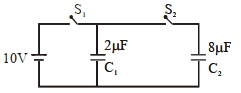
- 4$2\, \mu F$ વાળા $C _{1}$ કેપેસીટરને $10\, V$ ની બેટરી વડે ચાર્જ કરવામાં આવે છે. ત્યારબાદ બેટરી દૂર કરીને $8\, \mu F$ વાળા $C _{2}$ કેપેસીટરને $C _{1}$ સાથે જોડવામાં આવે છે. તો સંતુલન સમયે $C _{2}$ કેપેસીટર પરનો વિદ્યુતભાર ............ $\mu C$ હશે?View Solution
- 5$10^{-6} \mu \mathrm{C}$ નો એક વીજભાર $X-Y$ યામ પધ્ધતિના ઉગમબિંદુ $(0,0) \mathrm{m}$ પર મૂકેલો છે. બિંદુઓ $\mathrm{P}$ અને $\mathrm{Q}$ અનુક્રમે $(\sqrt{3}, \sqrt{3}) \mathrm{m}$ અને $(\sqrt{6}, 0) \mathrm{m}$ પર રહેલા છે. બિંદુઓ$\mathrm{P}$ અને $\mathrm{Q}$ વચચેનો સ્થિતિમાન તફાવત_____થશે.View Solution
- 6$2\,\mu F$ ના $7$ કેપેસિટરને નીચેની કઇ આકૃતિ પ્રમાણે જોડવાથી સમતુલ્ય $\frac{{10}}{{11}}\,\mu F$ કેપેસિટન્સ મળે?View Solution
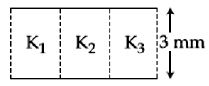
- 7એક સમાંતર પ્લેટ કે પેસિટરનું ક્ષેત્રફળ $6\, cm^2$ અને પ્લેટો વચ્ચેનું અંતર $3\,mm$ છે. $K_1 =10, K_2 =12, K_3 =14$ જેટલો પરાવૈધૃતાંક (ડાયઇલેક્ટ્રિક અચળાંક) ધરાવતા અને સમાન જાડાઇ ધરાવતા અવાહક પદાર્થની મદદથી બે પ્લેટો વચ્ચેના ગેપને ભરવામાં આવે છે (આકૃતિ જુઓ). જ્યારે અવાહકને પૂર્ણ તરીકે કેપેસિટરમાં દાખલ કરવામાં આવે અને જો સમાન કેપેસિન્ટસ (સંઘારક્તા) મળે તો પદાર્થનો ડાયઇલેક્ટ્રિક અચળાંક કેટલો હશે.View Solution
- 8કેપેસિટરની બે પ્લેટ વચ્ચે હવા હોેય ત્યારે તેનું કેપેસિટન્સ $1\,pF$ છે.બે પ્લેટ વચ્ચેનું અંતર બમણું કરી તેમની વચ્ચે મીણથી ભરી દેતા નવો કેપેસિટન્સ $2\,pF.$ છે. તો મીણનો ડાયઇલેકટ્રીક અચળાંક કેટલો હશે?View Solution
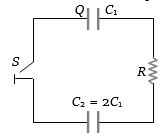
- 9જયારે કળ ખુલ્લી હોય,ત્યારે $C_1$ પર વિદ્યુતભાર $Q$ છે.જયારે કળ બંધ કરવામાં આવે,ત્યારે $C_1$ અને $C_2$ પર વિદ્યુતભાર કેટલો થાય?View Solution
- 10બે કેપેસિટરો $C_1$ અને $C_2$ ને અનુક્રમે $120\ V$ અને $200\ V$ ચાર્જ કરેલ છે. તે જાણવામાં આવ્યું છે કે બંનેને એકબીજાને જોડતાં દરેક એક પરનો સ્થિતિમાન શૂન્ય બનાવી શકાય તેથી.....View Solution
