$ 9.8 \times {10^{ - 3}}kg{m^{ - 1}} $ રેખીય દળ ધરાવતા તાર દ્વારા $30^°$ ના ઢાળવાળો ધર્ષણરહિત ઢાળ પર બે પદાર્થ આકૃતિ મુજબ બાંધેલા છે,તંત્ર સંતુલન સ્થિતિમાં હોય,ત્યારે તારમાં લંબગત તરંગની ઝડપ $100 m/s$ હોય, તો દળ $m$ કેટલું $m =$ ..... $kg$ હશે?
Difficult
Download our app for free and get started
a
(a) \(v = \sqrt {\frac{T}{\mu }} \)
(a) \(v = \sqrt {\frac{T}{\mu }} \)
For equilibrium \(Mg = mg \,sin 30 = T\)
==> \(M = \frac{m}{2}\)==> \(100 = \sqrt {\frac{{Mg}}{{9.8 \times {{10}^{ - 3}}}}} = \sqrt {\frac{{M(9.8)}}{{9.8 \times {{10}^{ - 3}}}}} \)
==> \(100 = \sqrt {M(1000)} \) ==> \(M = 10kg\) and \(m = 20kg\)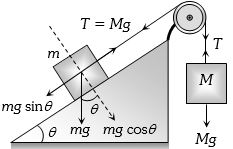
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક નિશ્વિત દોરી વિવિધ આવૃતિએ અનુનાદિત થાય છે. જેમમાંથી લઘુત્તમ $200 \,cps$ છે, તો પછીની કઈ ત્રણ ઉંચી આવૃતિએ તે અનુનાદ કરશે?View Solution
- 2$16$ સ્વરકાંટાને શ્રેણીમાં ગોઠવવામાં આવ્યા છે. દરેક સ્વરકાંટો તેના પહેલાના સ્વરકાંટા સાથે $ 8$ સ્પંદ ઉત્પન્ન કરે છે.છેલ્લા સ્વરકાંટાની આવૃતિ પહેલા કરતાં બમણી છે.તો પહેલા સ્વરકાંટાની આવૃતિ કેટલી થાય?View Solution
- 3નીચે ચાર સરળ આવર્તગતિ કરતાં તરંગ માટે સમીકરણ આપેલ છે.View Solution
$(i)\,\,\,\,\,{y_1} = A\,\cos \,\,2\pi \,\left( {{n_1}t\, + \,\frac{x}{{{\lambda _1}}}} \right)$
$(ii)\,\,\,\,\,{y_2} = A\,\cos \,\,2\pi \,\left( {{n_1}t\, + \,\frac{x}{{{\lambda _1}}} + \pi } \right)$
$(iii)\,\,\,\,\,{y_3} = A\,\cos \,\,2\pi \,\left( {{n_2}t\, + \,\frac{x}{{{\lambda _2}}}} \right)$
$(iv)\,\,\,\,\,{y_4} = A\,\cos \,\,2\pi \,\left( {{n_2}t\, - \,\frac{x}{{{\lambda _2}}}} \right)$
આપેલ પૈકી કઈ જોડી અનુક્રમે માધ્યમમાં વિનાશી વ્યતિકારણ અને સ્થિર તરંગો દર્શાવે છે
- 4$30\, m/s$ ના વેગથી ધ્વનિ ઉદ્ગમ ,ઉદ્ગમ અને અવલોકનકારને જોડતી રેખાને લંબ ગતિ કરે છે.ઉદ્ગમની આવૃત્તિ $n$ અને અવલોકનકારને સંભળાતી આવૃત્તિ $n +n_1$ છે.જો ધ્વનિનો વેગ $300 \,m/s$ હોય,તો નીચેનામાથી શું સાચું થાય?View Solution
એક વાહન જેના હોર્નની આવૃત્તિ $n$ છે તે અવલોકનકાર અને વાહનને જોડતી રેખાને લંબ દિશામાં $30\;m/s$ ના વેગ સાથે ગતિ કરે છે. અવલોકનકારને સંભળાતી આવૃત્તિ $n +n_1$ છે, તો (જો હવામાં ધ્વનિનો વેગ $300\;m/s$ છે)
- 5બે ઉદ્રગમ $A$ અને $B$ $660 \,Hz$ આવૃતિવાળો અવાજ ઉત્પન કરે છે. શ્રોતા અચથ વેગ $u$ સાથે $A$ થી $B$ તરફ ગતિ કરે છે. જો અવાજની ઝડપ $330\, m / s$ હોય તો એક સ્કન્ડમાં $8$ સ્પંદ સાંભળવા માટે $u$ ની કિંમત ........ $m / s$ હોવી જોઈએ.?View Solution
- 6...... $^oC$ તાપમાને હાઇડ્રોજનમાં ધ્વનિની ઝડપ $ 100^oC $ તાપમાને રહેલા ઓકિસજનમાં ધ્વનિની ઝડપ જેટલી થાય?View Solution
- 7$ {y_1} = A\sin (\omega t - kx) $ અને $ {y_2} = A\sin (\omega t - kx - \theta ) $ તરંગ સમાન દિશામાં ગતિ કરે છે,તો માધ્યમના કણનો કંપવિસ્તાર કેટલો થાય?View Solution
- 8સમાન તાપમાને રહેલા બે પાત્રમાં વાયુના અણુનું દળ $ m_1 $ અને $ m_2 $ છે.તો ધ્વનિની ઝડપનો ગુણોત્તર કેટલો થાય?View Solution
- 9એક ઘ્વનિ- તરંગની ગરમ હવામાં ઝડપ $350\; m/s $ પિત્તળમાં ઝડપ $3500\; m/s$ છે. જયારે તરંગ ગરમ હવામાંથી પિત્તળમાં પ્રસરણ પામે ત્યારે $ 700 \;Hz$ આવૃત્તિ ધરાવતા તરંગની તરંગલંબાઈ .....View Solution
- 10બે સિતારના તાર $A$ અને $B$ દ્વારા ‘ધ’ શબ્દ વગાડતા તે સ્પંદ ઉત્પન્ન કરે છે અને તેની આવૃતિ $5\,Hz$ મળે છે. જો $B$ તારમાં તણાવ થોડુક વધારવામાં આવે ત્યારે મળતા સ્પંદની આવૃતિમાં $3\,Hz$ જેટલો ઘટાડો થાય છે. જો $A$ ની આવૃતિ $425\,Hz$ હોય તો $B$ની મૂળભૂત આવૃતિ કેટલા $Hz$ હશે?View Solution