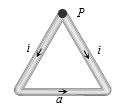
$'a' $ બાજુવાળા સમબાજુ ત્રિકોણમાં $i $ પ્રવાહનું વહન થાય છે.ત્રિકોણના બિંદુ $P$ પર ચુંબકીયક્ષેત્ર કેટલું થાય?
Medium
Download our app for free and get started
b
\((b) \) \({B_1} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2i\sin {{30}^o}}}{{\frac{{\sqrt 3 a}}{2}}}\) \( \odot \)
\((b) \) \({B_1} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2i\sin {{30}^o}}}{{\frac{{\sqrt 3 a}}{2}}}\) \( \odot \)
\( = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2i}}{{\sqrt 3 a}}\) \( \odot =\) \(\frac{{{\mu _0}i}}{{2\sqrt 3 \pi a}}\) \( \odot\)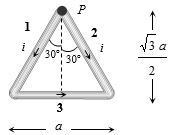
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$100$ આંટા અને $1 \,cm^2 $ ક્ષેત્રફળ ધરાવતા ગેલ્વેનોમીટરના કોઇલનો વળઅચળાંક $10^{-8 }\, N-m\, rad.$ છે.જો ચુંબકીયક્ષેત્ર $5 \,T$ હોય,તો પ્રવાહસંવેદીતા કેટલી થાય?View Solution
- 2$1000$ આંટા પ્રતિ મીટર ધરાવતા સોલેનોઇડની સાપેક્ષ પરમીએબિલિટી $500$ છે. સોલેનોઇડના ગૂચળામાંથી $5\, A$ નો પ્રવાહ વહેતો હોય તો સોલેનોઇડમાંથી ઉત્પન્ન થતું ચુંબકીયક્ષેત્ર કેટલું હશે?View Solution
$\left(\mu_0=4 \pi \times 10^{-7} H / m \right)$
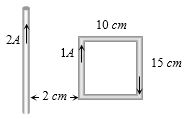
- 3View Solutionઆપેલ આકૃતિ માં રહેલ લૂપ પર કેટલું બળ લાગતું હશે?
- 4View Solutionજો સમાન વેગમાન ધરાવતો ઇલેક્ટ્રોન અને પ્રોટોન ચુંબકીયક્ષેત્રને લંબ પ્રવેશે, તો ...
- 5એક વિદ્યુતભાર માટે $q/m$ નું મૂલ્ય $10^8\, C/kg$ અને તે $3 \times 10^5\, m/s$ ના વેગથી $0.3\, T$ તીવ્રતાવાળા ચુંબકીયક્ષેત્રમાં, ક્ષેત્ર સાથે $30^o$ ના ખૂણે દાખલ થાય છે. વક્રાકાર માર્ગની ત્રિજયા ........ $cm$ હશે.View Solution
- 6$4.0 \mu \mathrm{C}$ નો વિદ્યુતભાર $4.0 \times 10^6 \mathrm{~ms}^{-1}$ ના વેગથી ધન $y$-અક્ષની દિશામાં $(2 \hat{k}) \mathrm{T}$ જેટલી પ્રબળતા ધરાવતા ચુંબકીય ક્ષેત્ર $\vec{B}$ ની અસર હેઠળ ગતિ કરે છે. વિદ્યુતભાર ઉપર લાગતું બળ $x \hat{i} N$ છે.. $x$ નું મૂલ્ય___________છે.View Solution
- 7એક લાંબી, સુરેખ અને પાતળી દિવાલવાળી પાઇપમાંથી વિદ્યુતપ્રવાહ $I$ વહે છે. તો નીચેનામાંથી ક્યું વિધાન સાયું છે?View Solution
- 8વેગ $\overrightarrow{\mathrm{u}}=3 \hat{\mathrm{i}}+5 \hat{\mathrm{j}} \mathrm{m} / \mathrm{s}$ અને ઈલેકટ્રોન પર લાગતું બળ $\vec{F}=5 \mathrm{ekN}$ છે. જ્યા e ઈલેકટ્રોન પરનો વિદ્યુતભાર છે. તો $B0$ નું મૂલ્ય .......... $T$View Solution
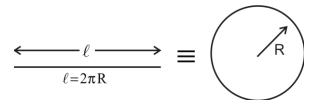
- 9$314\,cm$ લંબાઈ અને $14\,A$ નો પ્રવાહ ધરાવતા એક તારને વાળીને એક વર્તુળ બનાવવામાં આવે છે. ગૂંચળાની ચુંબકીય ચાકમાત્રા $..........A - m ^2$ હશે. [Given $\pi=3.14$ ]View Solution
- 10$5 \mathrm{eV}$ ગતિઊર્જા ધરાવતો એક ઈલેકટ્રોન $3 \mu \mathrm{T}$ ના નિયમિત ચુંબકીય ક્ષેત્ર ધરાવતા વિસ્તારમાં ક્ષેત્રની દિશાને લંબરૂપે દાખલ થાય છે. $E$ જેટલું વિદ્યુતક્ષેત્ર વેગની દિશા અને ચુંબકીય ક્ષેત્રની દિશાને લંબરૂપે લગાવવામાં આવે છે. ઇલેકટ્રોન ત જ માર્ગ ઉપર ગતિ ચાલુ રાખે તે માટે જરૂરી $E$નું મૂલ્ય. . . . . . $\mathrm{NC}^{-1}$ થશે. (ઇલેકટ્રોનનું દળ = $9 \times 10^{-31} \mathrm{~kg},$ ઈલેકટ્રોનનો વિદ્યુતભાર $= 1.6 \times 10^{-19} \mathrm{C}$ આપેલ છે.)View Solution