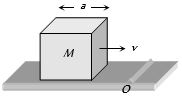
$a$ બાજુવાળો એક સમઘન નીચેની આકૃતિમાં દર્શાવ્યા પ્રમાણે એક સમક્ષિતિજ સમતલ પર $v$ વેગથી ગતિ કરે છે તે $O$ બિંદુ આગળ આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ઊપસેલી સપાટી પાસેથી પસાર થાય તો $O$ બિંદુ પછી તેનો કોણીય વેગ કેટલો થાય ?

IIT 1999, Medium
a
when block hits ridge at \(O\), it will start rotating about an axis passing through \(O\) and perpendicular to the plane of paper. No external torque acts on block hence angular momentum is conserved Angular momentum before hitting,
when block hits ridge at \(O\), it will start rotating about an axis passing through \(O\) and perpendicular to the plane of paper. No external torque acts on block hence angular momentum is conserved Angular momentum before hitting,
\(Li = M \cdot V \times AC\)
\(= MV \cdot( a / 2)=[( mva ) / 2]\)
after hitting, \(L_{f}=I_{0} \omega\)
\(I_{0}\) is MI of block about axis through \(O\) and perpendicular to plane of block.
if \(I_{c}\) is MI about \(C\) then \(I_{C}=\left[\left(M a^{2}\right) / 6\right]\)
From parallel axes theorem,
\(I_{0}=I_{c}+M r^{2}\)
and \(r^{2}=(a / 2)^{2}+(a / 2)^{2}=\left(a^{2} / 2\right)\)
\(I_{0}=(1 / 6) M a^{2}+(1 / 2) M a^{2}=(2 / 3) M a^{2}\)
\(L _{ f }=(2 / 3) Ma ^{2} \cdot \omega\)
also \(L _{ i }= L _{ f }\) hence
\([( mva ) / 2]=(2 / 3) Ma ^{2} \omega\) hence \(\omega=(3 v / 4 a )\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$60$નો કોણવાળા ઢાળવાળા સમતલ પર એક નળાકાર ગબડે છે. ગબડતી વખતે તેનો પ્રવેગ $\frac{x}{\sqrt{3}} \mathrm{~m} / \mathrm{s}^2$ છે, જ્યાં $x=$__________.$\left(g=10 \mathrm{~m} / \mathrm{s}^2 \mathrm{q}\right)$.View Solution
- 2એક તક્તી $\vec{\omega}$ કોણીય ઝડપથી ભ્રમણ કરી રહી છે. બ્રમણાક્ષની સાપેક્ષે સ્થાન સદિશ $\vec{r}$ ધરાવતાં બિંદુ પર $\vec{F}$ બળ લગાડવામાં આવે છે. તો આ બળ વડે ઉદભવતાં ટોર્કની સાથે જોડાયેલો પાવર શું થશે ?View Solution
- 3ઓટોમોબાઈલ એન્જિનમાં $ 6000\ rpm$ એ $ 200\ hp$ પાવર મળે છે તેને અનુરૂપ ટોર્ક ......... $N.m$ થશે.View Solution
- 4એક પાતળી વર્તુળાકાર રિંગ જેનું દળ $M$ અને ત્રિજ્યા $R$ તેની ધરી પર અચળ કોણીય વેગ $\omega $ થી પરિભ્રમણ કરે છે. રિંગનાં વ્યાસના બિંદુઓ પર $m$ દળનાં એવા બે પદાર્થોને ધીમેથી જોડવામાં આવે છે. હવે રિંગ કેટલા કોણીય વેગથી ગતિ કરશે?View Solution
- 5પૃષ્ઠને લંબ એવા કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $I_1$ જડત્વની ચાકમાત્રા ધરાવતી તકતી આ અક્ષને અનુલક્ષીને $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. હવે, પૃષ્ઠને લંબ એવા કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $I_2$ જેટલી જડત્વની ચાકમાત્રા ધરાવતી બીજી તકતી આ તકતી પર મૂકવામાં આવે, તો આ બંને તકતીનો સંયુક્ત કોણીય વેગ કેટલો હશે ?View Solution
- 6$1 \,kg$ દળ અને $10 \,cm$ ત્રિજ્યા વાળો એક પોલો ગોળો તેના વ્યાસને અનુલક્ષીને ભ્રમણ કરવા માટે મુક્ત છે. જો $30 \,N$ નું એક બળ સ્પર્શકીય રીતે તેની પર લગાડવામાં કરવામાં આવે તો તેનો કોણીય પ્રવેગ શું થાય? ( $rad / s ^2$ માં)View Solution
- 7$1\; \mathrm{m}$ લાંબા સળિયાનો એક છેડો સમક્ષિતિજ ટેબલ પર જડેલો છે.જ્યારે તે સમક્ષિતિજ સાથે $30^{\circ}$ નો ખૂણો બનાવે ત્યારે તેણે મુક્ત કરવામાં આવે છે.તે જ્યારે ટેબલ સાથે અથડાય ત્યારે તેનો કોણીય વેગ $\sqrt{\mathrm{n}}\; \mathrm{s}^{-1}$ આપવામાં આવે છે જ્યાં $\mathrm{n}$ એ પૂર્ણાંક સંખ્યા હોય તો $n$ મૂલ્ય કેટલું હશે?View Solution
- 8View Solutionસમાન દળ અને ત્રિજ્યાનો એક નક્કર નળાકાર અને એક નક્કર ગોળો એક ખરબચડા ઢોળાવ વાળા સમતલ ઉપર સરક્યાં વિના ગબડે છે. ઘર્ષણ નું બળ કેટલું થાય?
- 9એક પૈડાનો કોણીય પ્રવેગ $3 \;rad/s^2$ છે અને તેની પ્રારંભિક કોણીય ઝડપ $2\; rad/s $ છે. $2\;s$ માં તેણે કેટલા ખૂણાનું કોણીય સ્થાનાંતર ($rad $ માં) કર્યું હશે?View Solution
- 10એક પોલો ગોળો તેની સંમિત અક્ષને સમાંતર (અનુલક્ષીને) એક સમતલ સપાટી ઉપર ગબડે છે તેની ચાકગતિ ઉર્જા અને કુલ ગતિઉર્જાનો ગુણોતર $\frac{x}{5}$ છે. $x$ નું મૂલ્ય. . . . . . .હશે.View Solution
