$A$ જેટલો આડછેદનું ક્ષેત્રફળ, $2 \times 10^{11} \mathrm{Nm}^{-2}$ જેટલો સ્થિતિસ્થાપકતાં અંક અને $2 \mathrm{~m}$ લંબાઈ ના એક તારને શિરોલંબ બે દઢ આધારની વચ્ચે લટકાવવામાં આવે છે. જ્યારે તેના કેન્દ્રએ (મધ્યબિંદુુ) આગળ $2 \mathrm{~kg}$ નું દળ લટકાવવામાં આવે છે ત્યારે તે ખેચાયેલ તાર સાથે $\theta=\frac{1}{100} \operatorname{rad}$ નો આકૃતિમાં દર્શાવ્યા પ્રમાણે કોણ બનાવે છે. આડછેદ નું ક્ષેત્રફળ $\mathrm{A}$. . . . . . .$\times 10^{-4} \mathrm{~m}^2$ છે. ( $x < < L$ ધારો). (given; $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )
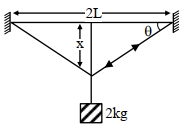

JEE MAIN 2024, Diffcult
c
In vertical derection \(2 \mathrm{~T} \sin \theta=20\)
In vertical derection \(2 \mathrm{~T} \sin \theta=20\)
using small angle approximation \(\sin \theta=\theta\)
\(\theta=\frac{1}{100}\)
\(\therefore \quad \mathrm{T}=\frac{10}{\theta}\)
\(T=1000 \mathrm{~N}\)
Change in length \(\Delta \mathrm{L} \quad=2 \sqrt{\mathrm{x}^2+\mathrm{L}^2}-2 \mathrm{~L}\)
\(=2 \mathrm{~L}\left[1+\frac{\mathrm{x}^2}{2 \mathrm{~L}^2}-1\right]\)
\(\Delta \mathrm{L} =\frac{\mathrm{x}^2}{\mathrm{~L}}\)
\(\therefore\) Modulus of elasticity \(=\frac{\text { stress }}{\text { strain }}\)
\(2 \times 10^{11}=\frac{10^3}{\mathrm{~A} \times \frac{\mathrm{x}^2}{\mathrm{~L}}} \times 2 \mathrm{~L}\)
\(\therefore \quad \mathrm{A}=1 \times 10^{-4} \mathrm{~m}^2\)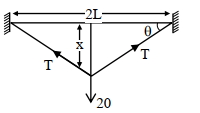
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1આકાર વિકૃતિ $\phi$ ના લીધેં પદાર્થના કદ $V$ માં સંગ્રહ થતી. વિકૃતિ ઉર્જા કેટલી ? (shear modulus is $\eta$ )View Solution
- 2$l$ લંબાઈ અને $A$ આડછેદ ધરાવતા સળિયાને $0°C$ થી $100°C$ સુધી ગરમ કરવામાં આવે છે. સળિયાને એવી રીતે મૂકેલો છે કે જેથી તેની લંબાઈમાં વધારો થવા દેવામાં આવતો નથી તો તેના પર ઊદભવતું બળ કોના સમપ્રમાણમાં હોય ?View Solution
- 3$1\, m^3$ કદ ધરાવતા પાણીને એક તળાવની સપાટીથી $200$ ઊંડાઈએ લઈ જવામાં આવે છે.જો પાણીનો બલ્ક મોડ્યુલસ $22000$ વાતાવરણ હોય તો તેના કદમાં કેટલો ફેરફાર થાય? (પાણીની ઘનતા $1\times10^3\, kg/m^3$, વાતાવરણનું દબાણ $= 10^5\, N/m^2$ અને $g = 10\, m/s^2$)View Solution
- 4જો સમુદ્રની સરેરાશ ઉંડાઈ $4000 \mathrm{~m}$ અને પાણીનો કદ સ્થિતિસ્થાપકતા અંક $2 \times 10^9 \mathrm{Nm}^{-2}$ હોય તો પાણીનું સમુદ્નના તળિયે આંશિક સંકોચન $\frac{\Delta V}{V}$ બરાબર $\alpha \times 10^{-2}$ છે. તો $\alpha$ નું મૂલ્ય__________છે. ( $\mathrm{g}=10 \mathrm{~ms}^{-2}, \rho=1000 \mathrm{~kg} \mathrm{~m}^{-3}$ આપેલ છે.)View Solution
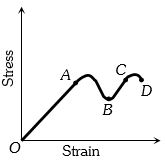
- 5નીચેના ગ્રાફમાં બિંદુ $B$ શું દર્શાવે છે.View Solution
- 6$60 \,cm$ ની બાજુ અને $15 \,cm$ ની જાડાઈ ધરાવતા એક ચોરસ એલ્યુમિનિયમ (મોડ્યુલ્સ આફ રીજીડીટી આકાર સ્થિતિસ્થાપકતા અંક $25 \times 10^{9} \,Nm ^{-2}$ )ને (તેની સાંકળી સપાટી બાજુ પર) $18.0 \times 10^{4} \,N$ જેટલું સ્પર્શીય બળ લગાડવામાં આવેલ છે. નાની બાજુને જમીન સાથે રીવેટથી જોડવામાં આવેલ છે. ઉપરની બાજુનું સ્થાનાંતર .......... $\mu m$ માં હશે.View Solution
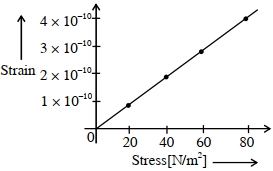
- 7દ્રવ્ય માટે તેની સ્થિતિસ્થાપક હદમાં રેખીય પ્રતિબળ અને રેખીય વિકૃતિનો આલેખ આકૃતિમાં દર્શાવેલ છે. $5 \times 10^{-4}$ જેટલી રેખીય વિકૃતિ માટે ઊર્જા ઘનતામાં થતો વઘારો ............ $kJ / m ^{3}$ હશે.View Solution
- 8જો સમુદ્રની સરેરાશ ઉંડાઈ $4000 \mathrm{~m}$ અને પાણીનો કદ સ્થિતિસ્થાપકતા અંક $2 \times 10^9 \mathrm{Nm}^{-2}$ હોય તો પાણીનું સમુદ્નના તળિયે આંશિક સંકોચન $\frac{\Delta V}{V}$ બરાબર $\alpha \times 10^{-2}$ છે. તો $\alpha$ નું મૂલ્ય__________છે. ( $\mathrm{g}=10 \mathrm{~ms}^{-2}, \rho=1000 \mathrm{~kg} \mathrm{~m}^{-3}$ આપેલ છે.)View Solution
- 9$8 \,m$ લાંબી રબરની નળી જેની ઘનતા $1.5 \times {10^3}\,N/{m^2}$ અને યંગ મોડ્યુલસ $5 \times {10^6}\,N/{m^2}$ ને છત પર લટકાવેલ છે. તો પોતાના વજનને લીધે તેની લંબાઈમાં થતો વધારો કેટલો હોય ?View Solution
- 10View Solutionસ્ટીલનો યંગ મોડયુલસ, પિત્તળના યંગ મોડયુલસ કરતાં બમણો છે. સમાન લંબાઇ અને સમાન આડછેદનું ક્ષેત્રફળવાળા એક સ્ટીલ અને બીજા પિત્તળના તારને એક જ છત પરથી લટકાવેલ છે. જો બંને તારના છેડે વજન લટકાવવાથી નીચેના છેડાઓ એક જ સ્તર પર હોય, તો સ્ટીલ અને પિત્તળના તારોના છેડે લટકાવેલ વજનનો ગુણોત્તર કેટલો હોવો જોઇએ?
