Exercise - 1.28
Download our app for free and get started
SELF STUDY
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1अब ऐसा विश्वास किया जाता है, कि स्वयं प्रोटॉन एवं न्यूट्रॉन (जो सामान्य द्रव्य के नाभिकों का निर्माण करते हैं) और अधिक भूल इकाइयों जिन्हें क्वार्क कहते हैं के बने हैं। प्रत्येक प्रोटॉन तथा न्यूट्रॉन तीन क्वार्कों से मिलकर बनता है। दो प्रकार के क्वार्क होते हैं। अप क्वार्क (u) जिन पर $+\frac{2}{3} e$ आवेश तथा एक डाउन क्वार्क (d) जिस पर $-\frac{1}{3} e$ आवेश होता है। इलेक्ट्रॉन से मिलकर सामान्य द्रव्य बनाते हैं। (कुछ अन्य प्रकार के भी क्वार्क पाये जाते हैं। जो भिन्न असामान्य प्रकार के द्रव्य बनाते हैं) प्रोटॉन तथा न्यूट्रॉन के सम्भावित क्वार्क संघटन समझाइये।View Solution
- 2View Solution
- 3View Solution
- 4दो वैद्युत आवेशों के बीच स्थिर वैद्युत बल के लिए कूलॉम नियम तथा दो स्थिर बिंदु द्रव्यमानों के बीच गुरुत्वाकर्षण बल के लिए न्यूटन का नियम दोनों में ही बल आवेशों/द्रव्यमानों के बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।View Solution
- इन दोनों बलों के परिमाण ज्ञात करके इनकी प्रबलताओं की तुलना की जाए
- एक इलेक्ट्रॉन तथा एक प्रोटॉन के लिए, दो प्रोटॉनों के लिए।
- इलेक्ट्रॉन तथा प्रोटॉन में पारस्परिक आकर्षण के वैद्युत बल के कारण इलेक्ट्रॉन तथा प्रोटॉन के त्वरण आकलित कीजिए जबकि इनके बीच की दूरी $A(= 10^{-10} m)$ है।$(m_p= 1.67 \times 10^{-27} K, m_e = 9.11 \times 10^{-31} \ kg)$
- इन दोनों बलों के परिमाण ज्ञात करके इनकी प्रबलताओं की तुलना की जाए
- 5View Solution
- 6View Solution
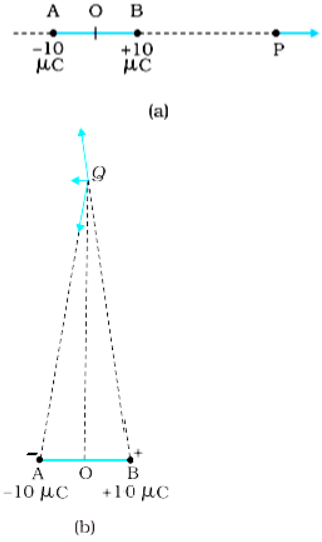
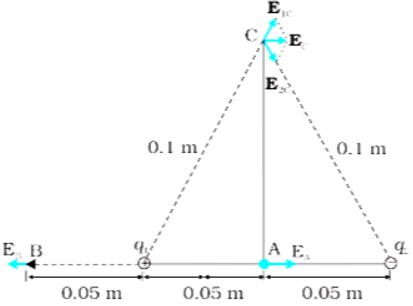
दो बिंदु आवेश $q_{1}$ तथा $q_2$ जिनके परिमाण क्रमश: $ +10^{-8} \mathrm{C}$ तथा $-10^{-8}C$ हैं एक दूसरे से $0.1\ m$ दूरी पर रखे हैं। चित्र में दर्शाए बिंदुओं $A, B$ तथा $C$ पर विद्युत क्षेत्र परिकलित कीजिए।
- 7अभ्यास 1.33 वर्णित कण की इलेक्ट्रान के रूप में कल्पना कीजिए जिसको $v_{x}=2.0 \times 10^{6}$ मी. /से. के साथ प्रक्षेपित किया गया है। यदि 0.5 सेमी. की दूरी पर रखी प्लेटों के बीच वैद्युत क्षेत्र E का मान 9.1$ \times 10^{2}$ न्यूटन/कूलॉम हो तो ऊपरी प्लेट पर इलेक्ट्रॉन कहाँ टकराएगा?View Solution
- 8यदि किसी पिंड से एक सेकंड में $10^9$ इलेक्ट्रॉन किसी अन्य पिंड में स्थानांतरित होते हैं तो $1C$ आवेश के स्थानांतरण में कितना समय लगेगा?View Solution
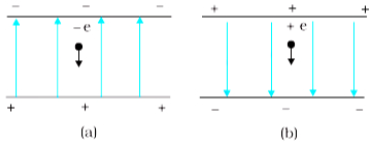
- 9प्रारम्भ में $x-$अक्ष के अनुदिश $v_x$ चाल से गति करती हुई दो आवेशित प्लेटों के मध्य क्षेत्र में $m$ द्रव्यमान तथा $-q$ आवेश का एक कण प्रवेश करता है। प्लेटों की लम्बाई $L$ है। इन दोनों प्लेटों के बीच एकसमान वैद्युत क्षेत्र $E$ बनाये रखा है। दर्शाइये कि प्लेट के अन्तिम किनारे पर व्यय का ऊधर्वाधर विक्षेप $\left(\frac{q E L^{2}}{2 m v_{x}^{2}}\right)$ हैं।View Solution
- 10View Solution
