When \({{\text{r}}_2} = {\text{C}},\) \(\angle {{\text{N}}_2}{\text{Rc}} = {90^o}\)
Where \(C=\) critical angle
As \(\sin C=\frac{1}{v}=\sin r_{2}\)
Applying snell's law at \('R'\)
\(\mu \,\,\sin {r_2} = 1\,\,\sin {90^o}\) ..... \((i)\)
Applying snell's law at \('Q'\)
\(1 \times \sin \theta=\mu \sin r_{1}\) ...... \((ii)\)
But \(r_{1}=A-r_{2}\)
So, \(\sin \theta=\mu \sin \left(A-r_{2}\right)\)
\(\sin \theta=\mu \sin A \cos r_{2}-\cos A\) ...... \((iii)\) [using \((i)\) ]
From \(( 1 )\)
\(\cos r_{2}=\sqrt{1-\sin ^{2} r_{2}}=\sqrt{1-\frac{1}{\mu^{2}}}\) ..... \((iv)\)
By eq. \((iii)\) and \((iv)\)
\(\sin \theta=\mu \sin A \sqrt{1-\frac{1}{\mu^{2}}}-\cos A\)
on further solving we can show for raynot to transmitted through face \(AC\)
\(\theta=\sin ^{-1}\left[u \sin \left(A-\sin ^{-1}\left(\frac{1}{\mu}\right)\right]\right.\)
So, for transmission through face \(\mathrm{AC}\)
\(\theta > {\sin ^{ - 1}}\) \(\left[ {u\sin \left( {A - {{\sin }^{ - 1}}\left( {\frac{1}{\mu }} \right)} \right]} \right.\)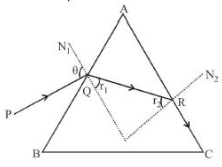
Download our appand get started for free
Similar Questions
- 1$20 \;cm$ ની કેન્દ્રલંબાઈ વાળા બહિર્ગોળ અરીસાને કારના "સાઈડ-વ્યુ મીરર” તરીકે ફીટ કર્યો છે. આ કારથી $2.8\;m$ પાછળ રહેલી બીજી કાર $15 \;m / s$ ની સાપેક્ષ ઝડપથી પ્રથમ કારને ઓવરટેક કરે છે. તો પ્રથમ કારનાં "સાઈડ-વ્યુ મીરર" માં દેખાતી બીજી કારનાં પ્રતિબિંબની ઝડ૫ કેટલી હશે?View Solution
- 2View Solutionજો તરંગ ધટ્ટ માધ્યમમાં વક્રીભવન અનુભવે તો નીચેનામાંથી કયું સાયું છે?
- 3સામાન્ય આંખ માટે, આંખની કોર્નિયાની અભિસારી ક્ષમતા $40\;D$ અને કોર્નિયાની પાછળના નેત્રમણિની લઘુતમ અભિસારી ક્ષમતા $20\;D $ છે. આ માહિતીનો ઉપયોગ કરતાં, નેત્રપટલ અને કોર્નિયાની નેત્રમણિ વચ્ચેનું અંતર($ cm$ માં) અંદાજીત કેટલું હશે?View Solution
- 4View Solutionઓપ્ટિકલ ફાઇબર કયાં સિદ્વાંત પર કાર્ય કરે છે?
- 5વસ્તુથી $90\, cm$ દૂર એક પડદો રાખ્યો છે. એકબીજાથી $20\, cm$ અંતરે આવેલા હોય તેવા બે સ્થાનો આગળ વારાફરતી એક બહિર્ગોળ લેન્સ મુકતાં પ્રતિબિંબ તે જ પડદા પર મળે છે. તો લેન્સની કેન્દ્રલંબાઈ શોધો.View Solution
- 6દરેકની $f$ કેન્દ્રલંબાઈ હોય તેવા બે સમાન પાતળા સમ બહિર્ગોળ (equi-convex) કાચોને એકબીજાના સમ-અક્ષીય સંપર્કમાં એવી રીતે રાખવામાં આવે છે કે જેથી આ સંયુક્ત રચનાની કેન્દ્રલંબાઈ ${F_1}$ છે. જ્યારે આ બે કાચો વચ્ચેની જગ્યાને ગ્લિસરીન વડે ભરવામાં આવે (કે જેનો કાચ જેટલો જ વક્રિભવનાંક છે $(\mu - 1.5)$), ત્યારે સમતુલ્ય કેન્દ્રલંબાઈ ${F_2}$ છે. ${F_1}:{F_2}$ નો ગુણોત્તર કેટલો હશે?View Solution
- 7$1.5$વકીભવનાંકવાળા દ્વિ-બહિર્ગોળ લેન્સની હવામાં કેન્દ્ર લંબાઈ $20 \mathrm{~cm}$ છે. જ્યારે તેને$1.6$ વક્રીભવનાંક ધરાવતા પ્રવાહીમાં ડૂબાડવામાં આવે ત્યારે તેની કેન્દ્ર લંબાઈ__________થશે.View Solution
- 8સમબાજુ પ્રિઝમનો ક્રાંતિકોણ $45^o $ છે.આપાતકિરણ એકસપાટીને લંબ હોય,તો...View Solution
- 9એક વ્યક્તિ $-1.0$ ડાયપ્ટર પાવર ધરાવતા ચશ્માનો દૂરની વસ્તુ જોવા માટે અને $2.0$ ડાયપ્ટર પાવર ધરાવતા વાંચવાના કાચનો ઉપયોગ કરે છે. વ્યક્તિ માટે લઘુતમ દ્રષ્ટિ અંતર $..........\,cm$ હશે.View Solution
- 10પાતળા બહિર્ગોળ લેન્સ માટે વક્રતાત્રિજ્યા અનુકુમે $15 \mathrm{~cm}$ અને $30 \mathrm{~cm}$ છે. લેન્સની કેન્દ્ર લંબાઈ $20 \mathrm{~cm}$ હોય તો દ્રવ્યનો વક્રીભવનાંક. . . . . . . હશે.View Solution
