વિધાન $I:$ $ v$ કણ જેટલી ઝડપથી ગતિ કરતો અને $m$ દળ ધરાવતો એક બિંદુવ્ત કણ, $M$ દળ ધરાવતા અને સ્થિર બીજા બિંદુવ્ત કણ સાથે અથડામણ અનુભવે છે,શકય મહત્તમ ઊર્જા વ્યય $f$ $\left( {\frac{1}{2}m{v^2}} \right)$ સૂત્ર વડે આપી શકાય.જો f $=\left( {\frac{m}{{M + m}}} \right)$
વિધાન $II$ : અથડામણને અંતે જો બંને કણો એકબીજા સાથે જોડાઇ જાય,તો મહત્તમ ઊર્જા વ્યય થશે.
Maximum energy loss \(=\frac{{{P^2}}}{{2m}} - \frac{{{P^2}}}{{2\left( {m + M} \right)}}\)
\(\left[ {\because \,K.E. = \frac{{{P^2}}}{{2m}} = \frac{1}{2}m{v^2}} \right]\)
\( = \frac{{2{P^2}}}{{2m}}\left[ {\frac{M}{{\left( {m + M} \right)}}} \right] = \frac{1}{2}m{v^2}\left\{ {\frac{M}{{m + M}}} \right\}\)
Statement II is a case of perfectly inelastic collision.By comparing the equation given in statement I with abpve equation, we get
\(f = \left( {\frac{M}{{m + M}}} \right)\,instead\,of\,\left( {\frac{m}{{M + m}}} \right)\)
Hence statement \(I\) is wrong and statement \(II\) is correct.
Download our appand get started for free
Similar Questions
- 1View Solutionવિધાન: હેલિકોપ્ટર માં ફરજિયાતપણે બે પંખીયા તો હોવા જ જોઈએ.
કારણ: બંને પંખીયા હેલિકોપ્ટરનું રેખીય વેગમાન સંરક્ષે છે.
- 2શરૂઆતમાં ઉગમબિંદુ પર સ્થિર રહેલ એક $m$ દળની મોટરગાડીનું એન્જિન અચળ પાવર $P$ આપતા તે પ્રવેગી ગતિ કરે છે. તો તેનું સ્થાન સમયના વિધેય સ્વરૂપે કઈ રીતે દર્શાવી શકાય?View Solution
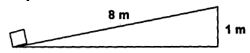
- 3$2 kg$ દળનો એક પદાર્થ આકૃતિમાં દર્શાવ્યા પ્રમાણે જેનો ઢાળ $8m$ અને ઉંચાઈ $1m $ હોય તેવા સમતલ પર સ્થિર સ્થિતિ એ છે ઘર્ષણ ગુમાંક $0.2$ હોય તો પદાર્થને ન્યૂનત્તમ બિંદુએથી મહત્તમ બિંદુએ પહોંચતા થતું કાર્ય કેટલા ....$J$ હશે ?View Solution
- 4$20 \,g$ દળની ગોળી $100 \,m / s$ પ્રારંભિક ઝડપથી રાઈફલમાંથી છૂટે છે અને એજ સ્તરે રહેલા લક્ષ્ય પર $50 \,m / s$ ઝડપથી લક્ષ્યને અથડાય છે. હવાનાં અવરોધ વડે થયેલ કાર્યની માત્રા ........ $J$ હશે.View Solution
- 5$0.01\; kg$ દળના પદાર્થનો વેગ $4\hat i + 16\hat k\; ms^{-1}$ થી $8\hat i + 20\hat j\,m{s^{ - 1}}$ થાય,તો થતું કાર્ય....$J$View Solution
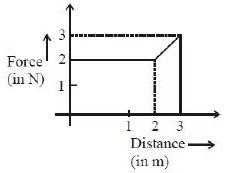
- 6ગ્રાફમાં દર્શાવ્યા પ્રમાણે એક કણ આપેલ સ્થાન સાથે બદલાતા બળના કારણે એક પારિમાણિક ગતિ કરે છે. $3\, m$ ગતિ કર્યા પછી કણની ગતિઉર્જા કેટલા .............. $\mathrm{J}$ થશે?View Solution
- 7એક હવામાં જતાં પદાર્થનો વેગ $(20 \hat{\mathrm{i}}+25 \hat{\mathrm{j}}-12 \hat{\mathrm{k}})$ છે તે અચાનક બે ભાગમાં વિભાજિત થાય છે જેમના દળનો ગુણોતર $1: 5$ છે.નાનો પદાર્થ $(100 \hat{\mathrm{i}}+35 \hat{\mathrm{j}} +8 \hat{\mathrm{k}})$ ના વેગથી ગતિ કરતો હોય તો મોટા પદાર્થનો વેગ કેટલો હશે?View Solution
- 8View Solutionવિધાન: બે બિલિયર્ડ દડાના સ્થિતિસ્થાપક સંઘાત માં ટૂંકાગાળાના દોલન દરમિયાન (જ્યારે તેઓ સંપર્કમાં હોય ત્યારે) કુલ ગતિઉર્જાનું સંરક્ષણ થાય છે.
કારણ: ઘર્ષણ વિરુદ્ધ વપરાયેલ ઉર્જા એ ઉર્જા સંરક્ષણના નિયમ ને અનુસરતી નથી.
- 9એક પદાર્થ પર લાગતું બળ $ F(x) = - kx + a{x^3} $ હોય,તો $ x \ge 0 $ માટે પદાર્થની સ્થિતિઊર્જાનો આલેખ નીચે પૈકી કયો થશે?View Solution
- 10$1250 kg$ ની કાર $30m/s$ ના વેગથી ગતિ કરે છે.$750N$ નું અવરોધક બળ લાગે છે.જો એન્જિન $30kW$ પાવર ઉત્પન્ન કરે,તો કારનો પ્રવેગ કેટલા ............... $\mathrm{m} / \mathrm{s} ^{2}$ થાય?View Solution
