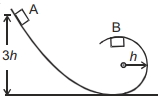
આકૃતિ માં દર્શાવ્યા મુજબ, એક પદાર્થને લીસા ટ્રેક ઉપર $A$ સ્થાને થી છોડવામાં આવે છે. જ્યારે પદાર્થ $B$ પર પહોંચે છે, ત્યારે ટ્રેક વડે તેના પર લાગેલ લંબપ્રતિક્રિયા બળ ....... છે?
Medium
Download our app for free and get started
b
(b)
(b)
Using Mechanical energy conservation
\(m g(3 h)=m g(2 h)+\frac{1}{2} m u^2\)
\(m g h=\frac{1}{2} m v^2\)
\(v^2=2 g h\)
\(m g+N=\frac{m v^2}{h}=\frac{m(2 g h)}{h}\)
\(N=m g\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્થિર સ્થિતિમાં રહેલો એક કણ એ $x$ અને $y$ દળનાં બે કણોમાં વિસ્ફોટ પામે છે. જેઓ એકબીજાથી વિરુદ્ધ દિશામાં $v_1$ અને $v_2$ વેગ સાથે ગતિ કરે છે. તેમની ગતિઉર્જાઓ $\left(E_1: E_2\right)$ નો ગુણોત્તર છેView Solution
- 2$0.5\; kg$ નો એક પદાર્થ સીધી રેખામાં વેગ $v=a x^{3 / 2}$ થી જાય (મુસાફરી કરે) છે, જ્યાં $a=5\; m ^{-1 / 2} s ^{-1}$.તેના $x=0$ થી $x=2\; m $ સ્થાનાંતર દરમિયાન પરિણામી બળ વડે કેટલું કાર્ય થયું હશે?View Solution
- 3એક $R$ ત્રિજ્યાનો લીસો ગોળો એક સુરેખ રેખા પર અચળ પ્રવેશ $a = g$ થી ગતિ કરે છે. એક કણને ગોળાના ઉપરના ભાગમાં રાખેલો છે. તેને ત્યાંથી ગોળાની સાપેક્ષે શૂન્ય વેગથી મુક્ત (છોડવામાં) કરવામાં આવે છે. કણ સરકે છે તે દરમિયાન ખૂણા $\theta$ ના વિધેયમાં ગોળાની સાપેક્ષે તેની ઝડપ કેટલી હશે?View Solution
- 4$4 \,m$ ઊંચી ઢોળાવવાળી સપાટી પર $5 \,kg$ દળ ધરાવતાં બ્લોકને ઉપર તરફ ખસેડવા માટે $250 \,J$ જેટલું કાર્ય થયું હોય તો, ઘર્ષણ વિરુદ્ધ થયેલ કાર્યનું મૂલ્ય .......... $J$ છે. $\left(g=10 \,ms ^{-2}\right)$View Solution
- 5$ 2.05 \times {10^6}\;kg $ દળ ધરાવતી ટ્રેનનો વેગ $5\; min$ માં $ 5\;m/s $ થી $25\; m/s $ થાય છે,તો એન્જિનનો પાવર કેટલા ......... $MW$ હશે?View Solution
- 6$'m' $ દળનો એક બોલ $'u'$ ઝડપથી હેડઓન સ્થિતિ સ્થાપક સંઘાતની અસર હેઠળ સ્થિર સ્થિતિએ રહેલા $(nm)$ દળના બોલને અથડાય છે. આ ઘટના દરમિયાન વજનદાર બોલમાં વહન પામતી ઘર્ષણઊર્જા કેટલી હશે ?View Solution
- 7$r$ ના વિધેયમાં સ્થિતિ ઊર્જા $U=\frac{A}{r^{10}}-\frac{B}{r^{5}}$ વડે આપવામાં આવે છે, જેમાં $r$ એ આંતરપરમાણીય અંતર, $A$ અને $B$ ધન અચળાંકો છે. બે પરમાણુ વચ્ચેનું સંતુલન અંતર...... હશે.View Solution
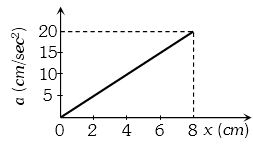
- 8$10 kg$ ના પદાર્થનો પ્રવેગ વિરુધ્ધ સ્થાનનો આલેખ આપેલ છે.તો $ x = 0 $ થી $ x = 8\,cm $ દરમિયાન કેટલું કાર્ય થશે?View Solution
- 9એક બોટ ને અચળ વેગે ચલાવવા માટે લાગતું જરૂરી બળએ તેની ઝડપના વર્ગના સમપ્રમાણમાં છે. જો $v\; km / h$ ઝડપ ને $4 \;kW$ પાવરની જરૂર હોય, તો $2v\; km / h$ ઝડપ ને ........... $kW$ પાવર જરૂર પડશે ?View Solution
- 10$6.4\,m$ ત્રિજયા ધરાવતા પોલા ગોળાની અંદર, નીચેના બિંદુથી બાઇકને એક પરિભ્રમણ પૂરું કરવા માટે જરૂરી લઘુત્તમ વેગ .......... $m/s$ હશે.View Solution