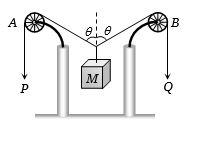
આકૃતિમાં બતાવ્યા પ્રમાણે ખેંચી ન શકાય તેવી સ્પ્રિંગ ના છેડાઓ $P$ અને $Q$ નિયમિત ઝડપ $ U$ થી નીચે તરફ ગતિ કરે છે. ગરગડીઓ $A$ અને $B$ ને સ્થિત કરેલી છે. તો દળ $M$ એ ઉપર તરફ કેટલી ઝડપે ગતિ કરશે?

IIT 1982, Diffcult
d
As \(P\) and \(Q\) fall down, the length l decreases at the rate of \(U \,m/s.\)
As \(P\) and \(Q\) fall down, the length l decreases at the rate of \(U \,m/s.\)
From the figure, \({l^2} = {b^2} + {y^2}\)
Differentiating with respect to time
\(2l \times \frac{{dl}}{{dt}} = 2b \times \frac{{db}}{{dt}} + 2y \times \frac{{dy}}{{dt}}\) \(\left( {{\rm{As \,\,}}\frac{{db}}{{dt}} = 0,\frac{{dl}}{{dt}} = U} \right)\)
\(⇒\) \(\frac{{dy}}{{dt}} = \left( {\frac{l}{y}} \right) \times \frac{{dl}}{{dt}}\) \( \Rightarrow \frac{{dy}}{{dt}} = \left( {\frac{1}{{\cos \theta }}} \right) \times U = \frac{U}{{\cos \theta }}\)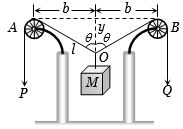
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionજ્યારે કોઈ પદાર્થ સંતુલન સ્થિતિમાં હોય ત્યારે,
- 2સ્થિર પડેલ બૉમ્બ એકાએક ફાટતાં તેના ત્રણ સરખા ટુકડા થાય છે. બે ટુકડાઓ એકબીજાને પરસ્પર એવી લંબદિશામાં $9\ m s^{-1}$ અને $12\ m s^{-1}$ ના વેગથી ગતિ કરે છે. ત્રીજા ટુકડાના વેગનું મૂલ્ય ....... $ms^{-1}$View Solution
- 3$10 \,kg$ દળને $5 \,m$ લાંબા દોરડાની મદદથી છત પરથી શિરોલંબ રીતે લટકાવવામાં આવેલ છે. દોરડાંના મધ્યબિંદુ આગળ $30 \,N$ જેટલું બળ સમક્ષિતિજ દિશામાં લગાવવામાં આવે છે. દોરડાનો શિરોલંબ સાથેનો કોણ $\theta=\tan ^{-1}\left(x \times 10^{-1}\right)$ છે. $x$ નું મૂલ્ય ........... થશે. $\left(g=10 m / s ^{2}\right)$View Solution
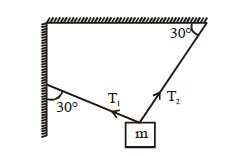
- 4$T_1$ અને $T_2$ શોધો.View Solution
- 5$M$ દળ અને $L$ લંબાઈની એકરૂપ દોરીને તેનાં ઉપરનાં સંતિમ છેડાને દઢ આધાર સાથે શિરોલંબ રીતે જોડેલ છે. તો પછી દઢ આધારથી $l$ અંતર પર દોરીમાં ઉદભવતો તણાવ શોધો.View Solution
- 6એક લિફ્ટની છત પર સ્પ્રિંગ બેલેન્સ ગોઠવેલ છે.જયારે લિફ્ટ સ્થિર હોય ત્યારે એક માણસ પોતાની બેગ આ બેલેન્સ પર લટકાવે છે ત્યારે તેનું વજન $49\, N$ નોંધાય છે,તો લિફ્ટ જયારે $5 ms^{-2}$ ના પ્રવેગથી અધોદિશામાં ગતિ કરે ત્યારે આ બેગનું વજન ......... $N$ નોંધાશે.View Solution
- 7$2 \,kg$ નો પદાર્થ સમક્ષિતિજ સપાટી પર $4 \,m/sec$ ના વેગથી ગતિ શરૂ કરતાં $2 \,sec$ પછી સ્થિર થઇ જાય છે.હવે આ પદાર્થને $4 \,m/sec$ ના અચળ વેગથી ગતિ કરાવવા માટે ........ $N$ બળ લગાવવું પડે.View Solution
- 8View Solutionનીચેનામાથી કયો બળો માટે ક્રમ સાચો છે?
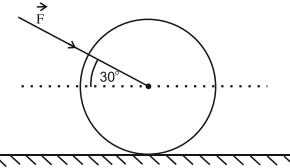
- 9આકૃતિમાં દર્શાવ્યા અનુસાર, એક $70\,kg$ દળ ધરાવતા, બગીચામાં વપરાતા, રોલરને સમક્ષિતિજ સાથે $30^{\circ}$ ના કોણે $\vec{F}=200\; N$ ના બળ વડે ધક્કો મારવામાં આવે છે. રોલર ઉપર લંબ પ્રતિબળ $...........\,N$ થશે. ( $g=10\,m s ^{-2}$ લો.)View Solution
- 10એક બંદૂક $50 \,gm$ દળની ગોળી $30\,m\,{\sec ^{ - 1}}$ વેગથી છોડે છે. તેના લીધે બંદૂક $1\,m\,{\sec ^{ - 1}}$ વેગથી પાછળ તરફ ધકેલાય છે. તો બંદૂકનું દળ .......... $kg$ હશે.View Solution
