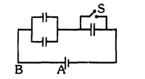
આકૃતિમાં દર્શાવેલ દરેક કેપેસિટર પાસે $5.0\ \mu F$ કેપેસિટન્સ છે. બેટરીનું $emf \,50\ V$ છે. જો $S$ સ્વિચને બંધ કરવામાં આવે તો $AB$ માંથી કેટલો વિદ્યુતભાર વહન પામશે ?

Diffcult
a
Initially when \(S\) is not connected
Initially when \(S\) is not connected
\(C_{\text {eff }} \frac{2 c}{3} q\)
\(=\frac{2 c }{3} \times 50\)
\(=\frac{5}{2} \times 10^{-4}\)
\(=1.66 \times 10^{-4}\,C\)
After the switch is made on
Then,
\(c_{\text {eff }}=2 c =10^{-6}\)
\(Q=10^{-6} \times 50\)
\(=5 \times 10^{-4}\,C\)
Now the initial charge will remain stored and in the stored in the short capacitor
Therefore,
Net charge flowing is
\(5 \times 10^{-4}-1.66 \times 10^{-4}\)
\(=3.3 \times 10^{-4}\,C\)
Hence, the net charge flows is \(3.3 \times 10^{-4}\,C\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
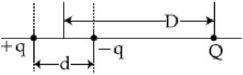
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે ત્રણ વિદ્યુતભાર મૂકેલા છે જો $D > > d$ હોય તો તંત્રનો વિદ્યુત સ્થિતિમાનનો તફાવત કેટલો થશે?View Solution
- 2View Solutionધાતુનો કવર ચડાવેલ દડો દોરી વડે બાંધીને બે પ્લેટની વચ્ચે લટકાવવામાં આવે છે.એક પ્લેટ ગ્રાઉન્ડ કરેલી છે,અને બીજી પ્લેટ ઘન વોલ્ટેજે રાખેલી છે.તો ...
- 3$a$ બાજુવાળા ચોરસના શિરોબિંદુ પર $Q$ વિજભાર મૂકવામાં આવે છે. ચોરસના કેન્દ્રથી $-Q$ વિજભારને અનંત અંતરે લઈ જવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 4જ્યારે સમાંતર પ્લેટ વચ્યે $d$ જાડાઈનું હવાનું માધ્યમ હોય ત્યારે તેનું કેપેસીટન્સ $5\,\mu\,F$ છે. આ બંને પ્લેટ વચ્યે $1.5$ ડાયઈલેક્ટ્રીક અચળાંક અને પ્લેટના ક્ષેત્રફળ જેટલું ક્ષેત્રફળ પણ $\frac{d}{2}$ જાડાઈ ધરાવતો પદાર્થ દાખલ કરવામાં આવે છે. તો સ્લેબની હાજરી કેપેસીટરનું કેપેસીટન્સ $..........\mu F$ થાય.View Solution
- 5$0.5$ કુલંબ વિદ્યુતભાર લઈ જતો નાનો છરો (બંદુકની ગોળી જેવો) $2000$ વોલ્ટનાં સ્થિતિમાનથી પ્રવેગીત કરવામાં આવે છે. તેની ગતિઊર્જા કેટલી થશે?View Solution
- 6જો સંધારક પરનો વિદ્યુતભાર $2\, C$ જેટલો વધારવામાં આવે તો તેમાં સંગ્રહીત ઊર્જા $44\%$ જેટલી વધે છે. સંધારક પરનો મૂળ વિદ્યુતભાર (કુલંબમાં)........હશે.View Solution
- 7$-10$ વોલ્ટ જેટલું સ્ચિતિમાન ધરાવતાં એક બિંદુ $V$ જેટલું સ્થિતિમાન ધરાવતાં એક બિંદુ પર $2C$ જેટલો ચાર્જને લાવવા માટે $50$ જુલ જેટલું કાર્ય કરવું પડતું હોય તો $V$ નું મુલ્ય $....$View Solution
- 8એક સંધારકની (કેપેસીટર) બે પ્લેટો વચ્યેનું અંતર $d$ છે અને જ્યારે પ્લેટ વચ્ચે હવાનું માધ્યમ હોય ત્યારે તેની સંધારકતા (કેપેસીટન્સ) $C_1$ છે. જો $\frac{2d}{3}$ જાડાઈ અને પ્લેટોના જેટલા જ ક્ષેત્રફળ વાળી ધાતુની તકતીને પ્લેટોની વચ્યે દાખલ કરવામાં આવે, તો સંધારકની સંધારકતા $C_2$ થાય છે. $\frac{C_2}{C_1}$ નો ગુણોત્તર ...... છે.View Solution
- 9કેપેસિટરને $V$ વૉલ્ટની બેટરી સાથે જોડેલ છે,તેના ડાઇઇલેક્ટ્રીક અચળાંક $k$ ધરાવતું માધ્યમ કેપેસીટરમાં દાખલ કરતાં કેપેસિટરમાં દાખલ કરતા કેપેસિટર પર નવો વિદ્યુતભાર .....View Solution
- 10એક વિદ્યુતભારિત ગોળાની અંદરનું સ્થિત વિદ્યુતસ્થિતિમાનનું સૂત્ર $\phi=$ $ar ^{2}+ b$ છે. જ્યાં $r =$ ગોળાના કેન્દ્રથી અંતર; $a,b$ અચળાંકો છે. ગોળાની અંદર વિદ્યુતભાર ઘનતા કેટલી હોય ?View Solution
