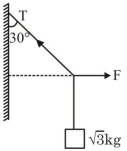
આકૃતિમાં દર્શાવ્યા અનુસાર, $4 \mathrm{~kg}, 6 \mathrm{~kg}$ અને $10 \mathrm{~kg}$ ના ત્રણ ચોસલાઓ $\mathrm{M}_1, \mathrm{M}_2$ અને $\mathrm{M}_3$ ને $1$, $2$ અને $3$ દોરડાં વડે ધર્ષણરહિત ગરગડી (પુલી) વડે લટકાવવામાં આવે છે. જ્યારે તેઓ ઉપરતરફ $2 \mathrm{~ms}^{-2}$ ના પ્રવેગથી ગતિ કરે છે ત્યારે દોરડા $1$ માં તણાવ $T_1$. . . . . . $\mathrm{N}$થશે. ( $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ લો.)
JEE MAIN 2024, Diffcult
Download our app for free and get started
d
\(FBD\) of \(M_1\) :
\(FBD\) of \(M_1\) :
\(\mathrm{T}_1-200=(4+6+10) \times 2\)
\(\therefore \mathrm{T}_1=240\)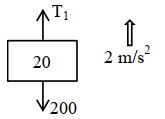
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક એલિવેટરની અંદર $2 \,kg$ અને $4 \,kg$ દળના બે બ્લોક્સ આદર્શ ગરગડી પરથી પસાર કરેલી દળરહિત દોરી વડ લટકાવેલાં છે. એલિવેટર એ $\frac{g}{2}$ પ્રવેગ સાથે ઉર્ધ્વ દિશામાં ગતિ કરી રહ્યો છે. બ્લોકો વચ્ચે જોડેલ દોરીમાં ઉદ્ભવવો તણાવ ............ $N$ હશે. $\left(g=10 m / s ^2\right.$ લો).View Solution
- 2એક પારંભિક સ્થિર યંત્ર એક ઘર્ધણઘર્ષણમુક્ત સપાટી પર પડ્યું છે. તે $2$ ટુકડાઓમાં ફાટે છે અને તે સપાટી પર ખસે છે. જો એક ટુકડો ધન $x$ દિશામાં ગતિ કરી રહ્યો હોય તો બીજો ટુક્ડો કઈ દિશામાં ગતિ કરશે ?View Solution
- 3એક માણસ એક હલકી દોરીથી નીચે લપસી રહ્યો છે જેની તૂટવાની શક્તિ એે માણસની વજનથી $\eta\;(\eta < 1)$ ગણી છે. તો માણસનો મહત્તમ પ્રવેગ શોધો કે જેથી દોરી તરત તૂટી જશે.View Solution
- 4બે જુદા-જુદા પ્રયોગોમાં $25 \,ms ^{-1}$ ની ઝડપથી ગતિ કરતો $5 \,kg$ દળનો એક પદાર્થ જુદી-જુદી દ્વિવાલોને અથડાય છે અને અનુક્રમે $(i) 3$ સેક્ન્ડ અને $(ii) 5$ સેકન્ડમાં વિરામસ્થિતિમાં આવે છે. નીચે આપેલામાંથી સાચો વિકલ્પ પસંદ કરો.View Solution
- 5$2 \,kg$ દળનો એેક પદાર્થ $4 \,m / s$ નાં અચળ વેગ સાથે ઘર્ષણ રહિત સમક્ષિતિજ ટેબલ પર ખસી રહ્યું છે. પદાર્થ ને એ જ વેગ સાથે ગતિમાં રાખવા માટે જરૂરી બળ ......... $N$ છે.View Solution
- 6$1 \;kg$ દળવાળા પદાર્થને ઊઘ્વૅ દિશામાં $100 \;m / s$ ના વેગથી ફેંકવામાં આવે છે. $5 \;seconds$ બાદ તે બે ટુકડાઓમાં વિભાજિત થાય છે. $400\; g$ દળવાળો એક ટુકડો અધોદિશામાં $25 \;m / s$ ના વેગથી ફેંકાય છે. બીજા ટુકડાના વેગની ગણતરી કરો?View Solution
- 7દોરડાનો એક છેડાને દળરહિત અને ઘર્ષણરહિત ગરગડી $P$ ઉપરથી પસાર થઈને એક હૂક સાથે બાંધવામાં આવે છે, જ્યારે બીજો છેડો મુક્ત હોય છે. દોરડુ મહત્તમ $360\; N$ તણાવ સહન કરી શકે છે. $60\,kg$ નો માણસ કેટલા મહત્તમ પ્રવેગથી ($m s^{-2}$ માં) દોરડા પર ચઢી શકે?View Solution
- 8$1000\, kg$ ની ટ્રોલી $50\, km/h$ ની ઝડપથી ઘર્ષણરહિત રસ્તા પર ગતિ કરે છે.તેમાં $250\, kg$ નો દળ મૂકતાં નવી ઝડપ ......... $km/hour$ થાય.View Solution
- 9$1 \mathrm{~m}$ લંબાઈનું સાદું લોલક $1 \mathrm{~kg}$ દળનું દોલક ધરાવે છે. તેના પર $10^{-2} \mathrm{~kg}$ દળની બુલેટ $2 \times 10^2 \mathrm{~ms}^{-1}$ ઝડપથી અથડાય છે. આ બુલેટ દોલકની અંદર ખૂંચી જાય છે. દોલકે પાછુ વળે તે પહેલાની ઉંચાઈ_______છે. ( $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$લો)View Solution
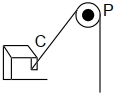
- 10દોરીના એક છેડે $\sqrt{3}$ દળ લગાડેલ છે. જ્યારે બીજો છેડો દિવાલ સાથે દોરીના એક છેડા સાથે દળ લગાડેલ છે જ્યારે બીજા છેડાને દીવાલ સાથે બાંધવામાં આવે છે. તેના પર અજ્ઞાત બળ $F$ એવી રીતે લગાડવામાં આવે છે કે જેથી દોરીતે દીવાલ સાથે $30^{\circ}$ નો ખૂણો બનાવે. તણાવ $T$ નું મૂલ્ય $........$ થાય. ($g$ નું મૂલ્ય $=10\,ms ^{-2}$)View Solution
