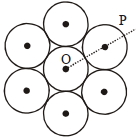
આકૃતિમાં દર્શાવ્યા અનુસાર દરેલ $M$ દળ ધરાવતી અને $R$ ત્રિજયાની સાત સમાન વર્તુળાકાર સમતલીય તકતીઓને સંમિતિમાં વેલ્ડીંગ કરેલ છે.સમતલને લંબ અને બિંદુ $P$ માંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા ________.

JEE MAIN 2018, Diffcult
c
Using parallel axes theorem, moment of inertia about \('O'\)
Using parallel axes theorem, moment of inertia about \('O'\)
\(\begin{array}{l}
{I_0} = {I_{cm}} + m{d^2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{7M{R^2}}}{2} + 6\left( {M \times {{\left( {2R} \right)}^2}} \right) = \frac{{55M{R^2}}}{2}
\end{array}\)
Again, moment of inertia about point P,\({I_P} = {I_0} + m{d^2}\)
\( = \frac{{55M{R^2}}}{2} + 7M{\left( {3R} \right)^2} = \frac{{181}}{2}M{R^2}\)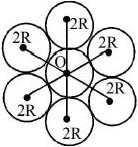
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1યામાક્ષ પધ્ધતિનાં ઉગમબિંદુ $O$ પર $- Fk$ જેટલું બળ લાગતું હોય તો $(1,-1)$ બિંદુ આગળ ટોર્ક કેટલું થાય?View Solution
- 2View Solutionપાતળી પોલો નળાકાર બંનેને છેડેથી ખુલ્લો છે. તે રોલિંગ કર્યા વિના સરકે છે અને પછી સરક્યા વિના તેટલી જ ઝડપથી રોલિંગ કરે છે બંને કિસ્સામાં ગતિ ઊર્જાનો ગુણોત્તર ........ થશે.
- 3એક $100\, m$ ઊંચા મકાનની ટોચ પર થી $0.03\, kg$ દળ ધરાવતા એક લાકડાના ટુકડાને મુક્ત કરવામાં આવે છે. આ જ સમયે, $0.02\, kg$ દળ ધરાવતી ગોળી (કારતુસ ) ને જમીન પરથી ઊર્ધ્વદિશામાં ઊપર તરફ $100 \,ms^{-1}$ ના વેગ થી છોડવામાં આવે છે. ગોળી લાકડામાં જોડાઈ જાય છે, તો આ સંયુક્ત તંત્રે પાછું પડવાનું ચાલુ કરે તે પહેલા મકાનની ટોચથી ઊપર પહોંચેલ મહત્તમ ઊંચાઈ ........ $m$ થશે. $(g=10 \,m/s^2)$View Solution
- 4એક મીટર સ્ટીકનો તેનાં એક છેડો તળીયા પર રહે તેમ શિરોલંબ રીતે મૂકવામાં આવે છે અને તેને છોડવામાં આવે છે, જ્યારે તેનો બીજો છેડો તળીયા સાથે અથડાય ત્યારે તેની ઝડપ ............... $m / s$ (ધારો કે તળીયા પર રહેલો છેડો લપસી જતો નથી.) $\left(g=9.8 \,m / s ^2\right)$View Solution
- 5View Solutionઅચળ કોણીય ઝડપથી ગતિ કરતું પૈડુ ગતિ દરમિયાન બ્રેકનો અનુભવે કરે તો તેની ચક્રાવર્તનની ત્રિજ્યા =…..
- 6$m$ દળના એક દઢ પદાર્થનું કોઈ એક અક્ષ ફરતે કોણીય વેગમાન તેના રેખીય વેગમાન $(P)$ થી $n$ ગણું છે. આ દઢ પદાર્થની કુલ ગતિઊર્જા કેટલી હશે?View Solution
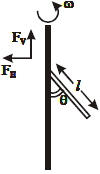
- 7$'l'$ લંબાઈના સળિયાને શિરોલંબ અક્ષ સાથે એક છેડાને જોડેલો છે,અક્ષ એ $w$ કોણીય ઝડપથી કરવાનું શરૂ કરે ત્યારે સળિયા અક્ષ સાથે $\theta$ ખૂણો બનાવે છે, દ્રવ્યમાન કેન્દ્રને અનુલક્ષીને સમક્ષિતિજ અને શિરોલંબ બળ $F_{H}$ અને $F_{V}$ દ્વારા મળતું ટોર્ક દ્વારા કોણીય વેગમાનનો ફેરફારનો સમયદર $\frac{ m \ell^{2}}{12} \omega^{2} \sin \theta \cos \theta$ મળે છે.તો $\theta$નું મૂલ્ય ..... .View Solution
- 8એક અક્ષ પર $I$ જડત્વની ચાક્માત્રા ધરાવતું પૈડું $\omega$ કોણીય ઝડપથી ભ્રમણ કરે છે.સ્થિર રહેલું $3I$ જડત્વની ચાકમાત્રા ધરાવતું પૈડું આ અક્ષ પર જોડવામાં આવે તો તંત્રની ગતિઊર્જામાં થતો આંશિક ઘટાડો છે.View Solution
- 9એક નિયમિત ઘનતાવાળી તકતી $10$ પરિભ્રમણ પ્રતિ સેકન્ડ કરે છે. તેની ઉપર ટૉર્ક લગાડતાં તેમાં $5\ rad s^{-2}$ નો કોણીય પ્રવેગ ઉત્પન્ન થાય છે.$2\ s $ બાદ તેનો કોણીય વેગ ......$ rad s^{-1}$ અને $2\ s$ માં તકતીએ કરેલાં પરિભ્રમણ ...... થાય.View Solution
- 10એક $W$ વજન ધરાવતા સળિયાને સમક્ષિતિજ સ્થિતિમાં સમતોલનમાં રહેલ બે તીક્ષ્ણ ધારો $A$ અને $B$ પર સમાંતરામાં મૂકેલ છે. તીક્ષ્ણ ધારો વચ્ચેનું એકબીજાથી અંતર $d$ છે. $A$ ધારથી સળિયાનું દ્રવ્યમાન કેન્દ્ર $x$ અંતરે છે. $A$ પરનું લંબબળ કેટલું હશે?View Solution
