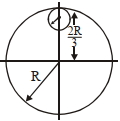
Let \(\sigma \) be the mass per unit area.
The total mass of the disc = \(\sigma \) \( \times \pi {R^2} = 9M\)
The mass of the circular disc cut
\( = \sigma \times \pi {\left( {\frac{R}{3}} \right)^2} = \,\sigma \times \frac{{\pi {R^2}}}{9} = M\)
Let us consider the above system as a complete disc of mass \(9M\) and a negative mass \(M\) super imposed on it. Moment of inertia \((I_1)\) of the complete disc = \(\frac{1}{2}9M{R^2}\) about an axis passing through \(O\) and perpendicular to the plane of the disc.
\(M.I.\) of the cut out portion about an axis passing through \(O'\) and perpendicular to the plane of disc \(=\) \(\frac{1}{2} \times M \times {\left( {\frac{R}{3}} \right)^2}\)
\(\therefore \,M.{\mathop{\rm I}\nolimits} .\left( {{I_2}} \right)\) of the cut out portion about an axis passing through \(O\) and perpendicular to the plane of disc
\( = \left[ {\frac{1}{2} \times M \times {{\left( {\frac{R}{3}} \right)}^2} + M \times {{\left( {\frac{{2R}}{3}} \right)}^2}} \right]\)
[Using perpendicular axis theorem]
\(\therefore \) The total \(M.I.\) of the system about an axis passing through \(O\) and perpendicular to the plane of the disc is
\(\begin{array}{l}
= \left[ {\frac{1}{2} \times M \times {{\left( {\frac{R}{3}} \right)}^2} + M \times {{\left( {\frac{{2R}}{3}} \right)}^2}} \right]\\
I = {I_1} + {I_2}\\
= \frac{1}{2}9M{R^2} - \left[ {\frac{1}{2} \times M \times {{\left( {\frac{R}{3}} \right)}^2} + M \times {{\left( {\frac{{2R}}{3}} \right)}^2}} \right]\\
= \frac{{9M{R^2}}}{2} - \frac{{9M{R^2}}}{{18}} = \frac{{\left( {9 - 1} \right)M{R^2}}}{2} = 4M{R^2}
\end{array}\)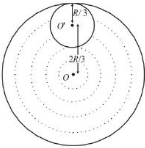
Download our appand get started for free
Similar Questions
- 1આકૃતિ માં બતાવ્યા પ્રમાણે $ABC$ એ નિયમિત તાર છે. જો તારનું દ્રવ્યમાન કેન્દ્ર બિંદુ $A$ થી શિરોલંબ દિશામાં નીચે તરફ છે તો $\frac{{BC}}{{AB}}$ એ શેની નજીક મળે?View Solution
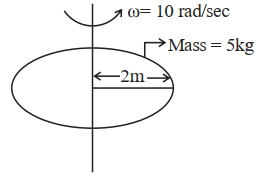
- 2એક $5 \mathrm{~kg}$ દળ, $2 \mathrm{~m}$ ત્રિજ્યા અને તેના પરિભ્રમણ સમતલને લંબ અક્ષને અનુરુપ કોણીય વેગ $10 \mathrm{rad} / \mathrm{sec}$ ધરાવતી એક તક્તિ ધ્યાનમાં લો. આ જ અક્ષની દિશામાં બીજી એક સમાન તક્તિને હળવેકથી ભ્રમણ કરતી તક્તિ ઉપર મૂકવામાં આવે છે. બંને તક્તિઓ સરક્યા સિવાય એકબીજા સાથે પરિભ્રમણ કરે તે માટે વિખેરીત થતી ઊર્જા_____________$j$ છે .View Solution
- 3$m$ અને $M$ $(M>m)$ ના દળોનું દ્રવ્યમાન કેન્દ્રView Solution
- 4$10 \,kg$ અને $30 \,kg$ દળ ઘરાવતા બે ચોસલાને સમાન સીધી રેખા પર અનુક્રમે $(0,0) \,cm$ અને $(x, 0) \,cm$ યામો આગળ મૂકવામાં આવેલા છે. $10 \,kg$ દળ ધરાવતા ચોસલાને સમાન રેખા ઉપર બીજા ચોસલા તરફ $6 \,cm$ જેટલો ખસેડવામાં આવે છે. દ્રવ્યમાન કેન્દ્રનું સ્થાન ન બદલાય તે માટે $30 \,kg$ ના ચોસલાને .......... અંતરે ખસેડવું જ પડશે.View Solution
- 5અચળ કદ $V$ ધરાવતા ગોળા ની જડત્વની ચાકમાત્રા $I$ હોય તો $I$ અને $V$ વચ્ચેનો સંબંધ ?View Solution
- 6$50 \mathrm{~cm}$ ત્રિજયા અને $2 \mathrm{~kg}$ દળ ધરાવતા બે સમાન ગોળાઓ એક હલકા સળીયાના બે છેડા સાથે જોડેલા છે જેથી તેમના કેન્દ્ર વચ્ચેનું અંતર $150 \mathrm{~cm}$ મળે છે. આ તંત્રની સળીયાના મધ્યબિંદુ માંથી પસાર થતી અને સળિયાની લંબાઈને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $\frac{x}{20} \mathrm{kgm}^2$ હોય તો $X$ નું મૂલ્ય ..........View Solution
- 7એક $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતીનું એકમ ક્ષેત્રફળ દીઠ દળ $\sigma (r) = kr^2$ મુજબ આપવામાં આવે છે જ્યાં $r$ એ તકતીના કેન્દ્રથી અંતર છે.તો તેના સમતલને લંબ અને દ્રવ્યમાન કેન્દ્રમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 8બિંદુ $ ( 2,-2,-2 )$ ને અનુલક્ષીને બિંદુ $( 2,0,-3 ) $ પર બળ $\overrightarrow {\;F} = 4\hat i + 5\hat j - 6\hat k$ ની ચાકમાત્રા આપવામાં આવે છે.View Solution
- 9View Solutionફલાય વ્હીલને એવી રીતે બનાવવામાં આવે છે જેથી તેનું સંપૂર્ણ દળ તેની રીમ પર સંકેન્દ્રિત થયેલું હોય છે, કારણ કે......
- 10એક ગાડીના પૈડાની કોણીય ઝડપ $360 \;rpm$ થી $1200 \;rpm$ થતાં $14 \;second$ લાગે છે તો તેની કોણીય પ્રવેગ મેળવોView Solution
