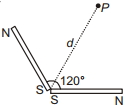
આકૃતિમાં દર્શાવ્યા મુજબ બે સરખાં નાના ગજિયા ચુંબકો $120^{\circ}$એ રાખેલ છે.દરેક ચુંબકની મેગ્નેટિક મોમેન્ટ $M$ છે. ખૂણાઓનાં દ્રિભાજકે $p$ બિંદુ એ ચુંબકીય ક્ષેત્ર
Medium
Download our app for free and get started
b
(b)
(b)
Since two equal vectors \(M\) are inclined at \(120^{\circ}\), their resultant will also be \(M\) and along its angular bisector. So point \(P\) is on axial line of resultant moment \(M\).
\(B_{ net }=\frac{2 \mu_0 M}{4 \pi d^3}\)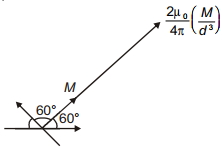
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક વિદ્યુતભારિત કણ (વિદ્યુતભાર $q$) $R$ ત્રિજયાના વર્તુળમાં એકસમાન ઝડપ $v$ થી ગતિ કરે છે. ચુંબકીય મોમેન્ટ $\mu $ શેના દ્વારા આપવામાં આવે છેView Solution
- 2એક નાના ગજિયા ચુંબકના કેન્દ્રથી $x$ અને $3 x$ જેટલાં અંતરે વિરુદ્ધ દિશામાં ચુંબકની અક્ષને લંબરૂપે $A$ અને $B$ બિંદુઓ આવેલા છે.તો $A$ અને $B$ બિંદુઓના ચુંબકીય ક્ષેત્રના ગુણોતરView Solution
- 3ડાયમેગ્નેટિક પદાર્થને $U- $ ટયુબમાં ભરવામાં આવે છે.હવે એક બાજુને ચુંબકીય ધ્રુવો વચ્ચે રાખતાં પ્રવાહી...View Solution
- 4પૃથ્વીની સપાટી પરના કોઈ એક બિંદુ $A$ પર નમનકોણ (angle of dip) $\delta = + 25^\circ $ છે. પૃથ્વીની સપાટી પરના બિંદુ $B$ પર નમનકોણ (angle of dip) $\delta = - 25^\circ $ છે. આપણે એમ સમજી શકીએ કે ...View Solution
- 5પૃથ્વીના ચુંબકીયક્ષેત્રનો સમક્ષિતિજ ઘટક $0.34×10^{-4} \,T $ ની અસર હેઠળ ટેન્જેન્ટ ગેલ્વેનોમિટરનું $ 30° $ કોણાવર્તન થતું હોય,તો કોઇલનું ચુંબકીયક્ષેત્રView Solution
- 6બે સમાન દળ ધરાવતા ચુંબકને આકૃત્તિ મુજબ રાખેલા છે.ચુંબક $1$ ની મેગ્નેટીક મોમેન્ટ ચુંબક $2$ કરતાં ત્રણ ગણી છે.તો સમતોલન સ્થિતિમાં ચુંબક $1$ એ મેગ્નેટિક મેરીડીયન સાથે કેટલો ખૂણો બનાવે?View Solution
- 7સમઅક્ષિય મૂકેલા બે ગજિયા ચુંબકના કેન્દ્ર વચ્ચેનું અંતર $r $ હોય,ત્યારે લાગતું બળ $4.8\, N $ છે.જો અંતર $ 2r$ કરવામાં આવે તો નવું બળ કેટલા ......$N$ થાય?View Solution
- 8એક ચુંબકીય સોયની લંબાઈની સાપેક્ષે તેની જાડાઈ અને પહોળાઈ અવગણી શકાય છે. જે સમક્ષિતિજ સમતલ સાથે $T$ સમયગાળા સાથે દોલનો કરે છે. આ સોયને લંબાઈને લંબરૂપે $n$ જેટલાં સરખાં ભાગોમાં તોડીએ તો દરેક ભાગનાં દોલનોનો સમયગાળોView Solution
- 9પેરામેગ્નેટિક પદાર્થની સાપેક્ષ પરમિએબિલિટી $\mu_r $ અને મેગ્નેટિક સસેપ્ટિબિલિટી $\chi $ કેવી હોય?View Solution
- 10બે સરખાં કદનાં ગજિયા ચુંબકોની મેગ્નેટિક મોમેન્ટોનો ગુણોત્તર $1: 2$ છે.જો તેમનાં ધ્રુવો સમાન રહે તે રીતે એકની ઉપર બીજો મુકીએ તો ચુંબકીય ક્ષેત્રમાં તે નાં દોલનોનો સમયગાળો $3s$ છે.જો એેકને ઉલટાવીએે તો આા ક્ષેત્ર માટે દોલન માટેનો સમયગાળોView Solution