એક વિદ્યુતભારિત કણ (વિદ્યુતભાર $q$) $R$ ત્રિજયાના વર્તુળમાં એકસમાન ઝડપ $v$ થી ગતિ કરે છે. ચુંબકીય મોમેન્ટ $\mu $ શેના દ્વારા આપવામાં આવે છે
AIPMT 2007, Medium
Download our app for free and get started
d
Magnetic moment \(\mu=I A\)
Magnetic moment \(\mu=I A\)
since \(T=\frac{2 \pi R}{v}\) Also, \(I=\frac{q}{T}=\frac{q v}{2 \pi R}\)
\(\therefore \quad \mu=\left(\frac{q v}{2 \pi R}\right)\left(\pi R^{2}\right)=\frac{q v R}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો ડાયમેગ્નેટિક પદાર્થ, પેરામેગ્નેટિક પદાર્થ , ફેરોમેગ્નેટિક પદાર્થના અણુની ચુંબકીય ચાકમાત્રા ${\mu _d},\,{\mu _p},\,{\mu _f} $ વડે દર્શાવાય, તો ....View Solution
- 2$1000$ આંટા$/m$ ધરાવતા લાંબા સોલેનોઇડના દ્રવ્યની સાપેક્ષ પરમીએબીલીટી $500$ અને કદ $10^{3}\, {cm}^{3}$ છે. જો તેનું કદ સમાન રાખીને તેને સાપેક્ષ પરમીએબીલીટી $750$ વાળા દ્રવ્યથી બદલી તેમાંથી સમાન પ્રવાહ $0.75\, {A}$ દાખલ કરવામાં આવે, તો કોરની ચુંબકીય મોમેન્ટમાં થતો આંશિક ફેરફાર $\left(\frac{{x}}{499}\right)$ છે. તો ${x}$ નું મૂલ્ય કેટલું હશે?View Solution
- 3ચુંબકની ચુંબકીય મોમેન્ટ $2.5\,J{T^{ - 1}}$ છે.તેને ચુંબકીયક્ષેત્ર $0.2\,T.$ માં સમતોલન સ્થિતિમાંથી અસ્થાયી સ્થિતિમાં લઇ જવા માટે કેટલા........$J$ કાર્ય કરવું પડે?View Solution
- 4View Solutionઅણુની ચુંબકીય મોમેન્ટ કયાં પદાર્થમાં શૂન્ય ન હોય?
- 5$0.2\, cm^2$ આડછેદવાળા લોખંડના સળિયામાં $1600 \,A-m^{-1}$ ની ચુંબકીય તીવ્રતાને લીઘે $2.4 \times 10^{-5 }\, Wb$ ફલકસ ઉત્પન્ન થાય છે. તો સળિયાની મેગ્નેટિક સસેપ્ટિબિલિટી કેટલી હશે?View Solution
- 6પૃથ્વીના ચુંબકીયક્ષેત્રનો સમક્ષિતિજ ઘટક $H$, શિરોલંબ ઘટક $V$ અને ડીપ $\delta$ વચ્ચેનો સંબંધ શું હશે? $( B_{E}=$ કુલ ચુંબકીય ક્ષેત્ર)View Solution
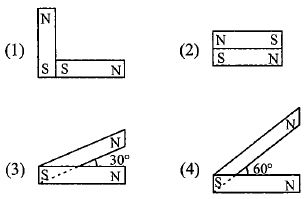
- 7નીચેની આકૃતિમાં ગજિયા ચુંબકની અલગ અલગ ગોઠવણી દર્શાવેલી છે. દરેક ચુંબકની ચુંબકીય ચાકમાત્રા $\vec m$ છે. કઈ ગોઠવણીની પરિણામી ચુંબકીય ચાકમાત્રા મહત્તમ થાય?View Solution
- 8View Solutionક્યુરીના નિયમને કઈ રીતે લખી શકાય?
- 9$2 \times {10^{ - 5}}\,{m^2}.$આડછેદવાળા લોખંડના સળિયામાં $2000 \,A/m $ ની ચુંબકીય તીવ્રતાને લીઘે $6.28 \times {10^{ - 4}}$ $weber$ ફલકસ ઉત્પન્ન થાય છે. તો સળિયાની પરમિએબિલિટી કેટલી હશે?View Solution
- 10$d$ બાજુઓનાં ચોરસનાં વિરદ્ધ ખૂણાઓએે બે નાના ગજિયા ચુંબકો જેમની મેગ્નેટિક મોમેન્ટ $M$ હોય તેમ રાખેલ છે.આમાં તેમનાં કેન્દ્રો ખૂણાઓ સાથે સુસંગત છે અને તેમની અક્ષો ચોરસની એક બાજુએ સમાંતર છે. જો સજાતીય ધ્રુવો એક દિશઆમાં હોય, તો ચોરસનાં કોઈપણ ખૂણાએ ચુંબકીય પ્રેરણView Solution