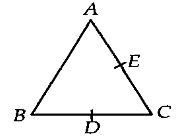
Here, \(A C=B C=2 a\)
\(D\) and \(E\) are the midpoints of \(B C\) and \(AC\).
\(\therefore A E=E C=a\) and \(B D=D C=a\)
\(\operatorname{In} \Delta A D C,(A D)^{2}=(A C)^{2}-(D C)^{2}\)
\(=(2 a)^{2}-(a)^{2}=4 a^{2}-a^{2}=3 a^{2}\)
\(A D=a \sqrt{3}\)
Similarly, potential at point \(D\) due to the given charge configuration is
\(V_{D}=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{q}{B D}+\frac{q}{D C}+\frac{q}{A D}\right]\)
\(=\frac{q}{4 \pi \varepsilon_{0}}\left[\frac{1}{a}+\frac{1}{a}+\frac{1}{\sqrt{3} a}\right]=\frac{q}{4 \pi \varepsilon_{0} a}\left[2+\frac{1}{\sqrt{3}}\right].........(i)\)
Potential at point \(E\) due to the given charge configuration is \(V_{E}=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{q}{A E}+\frac{q}{E C}+\frac{q}{B E}\right]\)
\(=\frac{q}{4 \pi \varepsilon_{0}}\left[\frac{1}{a}+\frac{1}{a}+\frac{1}{a \sqrt{3}}\right]=\frac{q}{4 \pi \varepsilon_{0} a}\left[2+\frac{1}{\sqrt{3}}\right].........(ii)\)
From the \((i)\) and \((ii)\), it is clear that
\(V_{D}=V_{E}\)
The work done in taking a charge \(Q\) from \(D\) to \(E\) is
\(W = Q({V_E} - {V_D}) = O\) \((\because \,{V_D} = {V_E})\)
Download our appand get started for free
Similar Questions
- 1$3\ F$ કેપેસીટન્સ ધરાવતા કેપેસીટરની પ્લેટનું ક્ષેત્રફળ કેટલુ હશે ? બે પ્લેટો વચ્ચેનું અંતર $5\, mm$ છે.View Solution
- 2$14\, pF$ કેપેસિટરને $V =12\, V$ની બેટરી સાથે લગાવેલ છે.બેટરી દૂર કરીને ડાઇઇલેક્ટ્રીક $k =7$થી કેપેસિટરને ભરતા તેની ઊર્જામાં થતો ફેરફાર $..........pJ$ થાય.View Solution
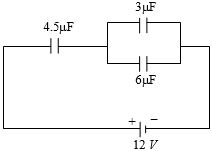
- 3આપેલ તંત્રમાં $4.5\ \mu\ F$ વચ્ચે વિધુતસ્થિતિમાનનો તફાવત કેટલા .....$V$ થાય?View Solution
- 4$6\ \mu F$ ક્ષમતા વાળા કન્ડેન્સરને $100\, V$ સુધી વિદ્યુતભારીત કરેલ છે તેને બીજા $14\ \mu F$ ક્ષમતા વાળા વિદ્યુતભાર રહીત કન્ડેન્સર સાથે જોડીને છોડી દેવામાં આવે છે. તો $6\ \mu F$ અને $14\ \mu F$ વાળા કન્ડેન્સર પરના વિદ્યુતભારોનો ગુણોત્તર તથા $6\ \mu F$ પરનો વિદ્યુત સ્થીતીમાન.....View Solution
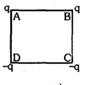
- 5આકૃતિમાં બતાવ્યા પ્રમાણે ચોરસના શિરોબિંદુઓ પર વિદ્યુતભાર મૂકેલા છે. વિદ્યુત ક્ષેત્ર $\mathop E\limits^ \to $ અને તેના કેન્દ્ર આગળનું સ્થિતિમાન $V$ લો. જો $A$ અને $B$ એ પરના વિદ્યુતભારોને $D$ અને $C$ અદલ બદલ કરવામાં આવે તો......View Solution
- 6બે સમાંતર ધાતુની પ્લેટની સમાન ધન ઘનતા $\left(\sigma=26.4 \times 10^{-12} C / m ^{2}\right)$ છે, તો બે પ્લેટ વચ્ચે વિદ્યુતક્ષેત્ર શોધો.View Solution
- 7$15 \,nF$ કેપેસિટરમાં ડાઈઇલેક્ટ્રીક અચળાંક $\varepsilon_{r}=2.5$ ડાઈઇલેક્ટ્રીક સ્ટ્રેન્થ $30 \,MV / m$ અને વિદ્યુતસ્થિતિમાન $=30\,V$ હોય તો પ્લેટનું ક્ષેત્રફળ .......... $\times 10^{-4} \;m ^{2}$ હશે?View Solution
- 8$0.2\,F$ કેપેસિટરને $600\,V$ ની બેટરી સાથે જોડેલ છે.હવે બેટરી દૂર કરીને $1\,F$ ના કેપેસિટર સાથે જોડતાં, નવો વોલ્ટેજ કેટલા........$volts$ થાય?View Solution
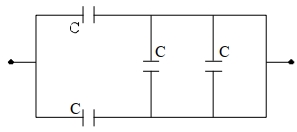
- 9View Solutionદર્શાવેલ સંયોજનની સમતુલ્ય સંધારકતા (કેપેસીટન્સ) ....... છે.
- 10$A$ ક્ષેત્રફળ અને $Q$ વિદ્યુતભાર ધરાવતા સમાંતર પ્લેટ કેપેસિટરની ઊર્જા ઘનતા કેટલી થાય?View Solution
