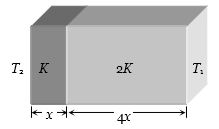
આકૃતિમાં દર્શાવ્યા પ્રમાણે એક સંયુકત બ્લોક બે જુદાં જુદાં બ્લોકોનું બનેલું છે.આ બે બ્લોકોની ઉષ્માવાહકતા અનુક્રમે $K$ અને $2K$ તથા તેમની જાડાઇ અનુક્રમે $x$ અને $4x$ છે.આ સંયુકત બ્લોકોના છેડાના તાપમાન $T_2$ અને $T_1 (T_2>T_1)$ છે.આ સંયુકત બ્લોકોમાંથી પસાર થતો ઉષ્માનો દર $ \left( {\frac{{A\left( {{T_1} - {T_2}} \right)k}}{x}} \right)f $ હોય,તો $f $ = _______

AIEEE 2004,AIIMS 2017, Diffcult
d
(d) Equation of thermal conductivity of the given combination \({K_{eq}} = \frac{{{l_1} + {l_2}}}{{\frac{{{l_1}}}{{{K_1}}} + \frac{{{l_2}}}{{{K_2}}}}} = \frac{{x + 4x}}{{\frac{x}{K} + \frac{{4x}}{{2K}}}} = \frac{5}{3}K\).
(d) Equation of thermal conductivity of the given combination \({K_{eq}} = \frac{{{l_1} + {l_2}}}{{\frac{{{l_1}}}{{{K_1}}} + \frac{{{l_2}}}{{{K_2}}}}} = \frac{{x + 4x}}{{\frac{x}{K} + \frac{{4x}}{{2K}}}} = \frac{5}{3}K\).
Hence rate of flow of heat through the given combination is \(\frac{Q}{t} = \frac{{{K_{eq}}.A({T_2} - {T_1})}}{{(x + 4x)}} = \frac{{\frac{5}{3}K\,A\,({T_2} - {T_1})}}{{5x}}\)=\(\frac{{\frac{1}{3}K\,A\,({T_2} - {T_1})}}{x}\) On comparing it with given equation we get \(f = \frac{1}{3}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1અમુક તાપમાને રહેલા પદાર્થમાંથી નીકળતા તરંગની મહત્તમ તરંગલંબાઇ $ {\lambda _o}. $ છે,જો પદાર્થનું તાપમાન વધારતાં મહત્તમ તરંગલંબાઇ $ \frac{{3{\lambda _o}}}{4} $ થાય છે. તો ઉત્સર્જન પાવર કેટલા ગણો વધે?View Solution
- 2કુકરની બનાવટમાં ઉપયોગી પદાર્થ હંમેશા કેવું જોઈએ? ($K -$ ઉષ્માવાહકતા, $S -$ વિશિષ્ટ ઉષ્મા)View Solution
- 3બે પદાર્થ $A$ અને $B$ જેનું વજન, ક્ષેત્રફળ અને બાહ્ય સપાટી એક સરખાં છે જેની વિશિષ્ટ ઉષ્મા $S_A$ અને $S_B\left(S_A > S_B\right)$ છે તેમને આપેલા તાપમાને ઠંડા પાડવામાં આવે છે તો સમય સાથે તાપમાનમાં કેટલો ફેરફાર થાય?View Solution
- 4$T$ તાપમાને રહેલા પદાર્થમાંથી નીકળતા તરંગની મહત્તમ તરંગલંબાઇ $\lambda_0$ છે,જો પદાર્થનું તાપમાન $ 2T $ કરતાં મહત્તમ તરંગલંબાઇ કેટલી થાય?View Solution
- 5જો મહત્તમ રેડીયેશન તરંગલંબાઈ તીવ્રતા સૂર્ય અને ચંદ્રની $0.5 \times 10^{-6} \,m$ અને $10^{-4} \,m$ હોય, તો તેના તાપમાનનો ગુણોત્તર કેટલો થાય?View Solution
- 6સમાન પરીમાણ ધરાવતા પાંચ સળિયાને આકૃતિ મુજબ જોડેલા છે. $A$ અને $B$ ને જુદાં જુદાં તાપમાને રાખતાં $CD$ માંથી ઉષ્માનું વહન થતું નથી,તોView Solution
- 7અમુક તાપમાને રહેલા પદાર્થમાંથી નીકળતા તરંગની મહત્તમ તરંગલંબાઇ $ 11 \times {10^{ - 5}}cm $ છે,જો પદાર્થનું તાપમાન $ n$ ગણું કરતાં મહત્તમ તરંગલંબાઇ $ 5.5 \times {10^{ - 5}}cm $ થાય છે. તો $n= $_____View Solution
- 8View Solutionસંપૂર્ણ સૂર્યગ્રહણ દરમિયાન ફોનહોફર રેખાઓ સ્પષ્ટ દેખાય છે કારણ કે.....
- 9જો $\lambda_{ m }$ એ $T\;K$ તાપમાને રહેલા કાળા પદાર્થમાંથી મહત્તમ ઉત્સર્જાતા વિકિરણની તરંગલંબાઈ દર્શાવે, તો .......View Solution
- 10જો સંપૂર્ણ કાળા પદાર્થનું તાપમાન $T$ થી $T/2 $ ઘટાડવામાં આવે ત્યારે ઉત્સર્જન દરમાં થતો ઘટાડો ...... $\%$ શોધો.View Solution
