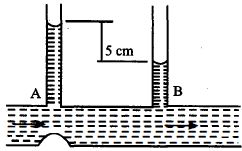
According to \(Bernoulli's\) theorem,
\({p_1} + \frac{1}{2}\rho v_1^2 = {P_2} + \frac{1}{2}\rho v_2^2\)
\(\therefore v_2^2 - v_1^2 = 2gh\) \(...\left( 1 \right)\)
According to the equation of continuty
\({A_1}{v_1} = {A_2}{v_2}\) \(...(2)\)
\(\frac{{{A_1}}}{{{A_2}}} = \frac{{6\,m{m^2}}}{{10\,m{m^2}}}\)
\(From\,equation\,\left( 2 \right),\frac{{{A_1}}}{{{A_2}}} = \frac{{{v_2}}}{{{v_1}}} = \frac{6}{{16}}\)
\(or,\,\,{v_2} = \frac{6}{{10}}{v_1}\)
Putting this value of \(v_2\) in equation \((1)\)
\({\left( {\frac{6}{{10}}{v_1}} \right)^2} - {\left( {{v_1}} \right)^2} = 2 \times {10^3} \times 5\)
\(\left[ \begin{array}{l}
g = 10m/{s^2} = {10^3}cm/{s^2}\\
and\,h = 5\,cm
\end{array} \right]\)
\(Solving\,we\,get\,{v_1} = \frac{{10}}{8}\)
Therefore the rate at which water flows through the tube
\( = {A_1}{v_1} = {A_2}{v_2} = \frac{{6 \times 10}}{8} = 7.5cc/s\)
Download our appand get started for free
Similar Questions
- 1$d,\,2d$ અને $3d$ ઘનતા ધરાવતા ત્રણ પ્રવાહી સમાન દળ લઇને મિશ્રણ કરવાથી, મિશ્રણની ઘનતા કેટલી થાય?View Solution
- 2ટાંકીમાં પાણીને $3 \,m$ ઊંચાઈ સુધી ભરવામાં આવે છે. ટાંકીનો આધાર જમીનથી ઉપર $1 \,m$ ઊંચાઈએ છે. કેટલી ઊંંચાઈ પર છિદ્ર બનાવવું જોઈએ કે જેથી પાણીને જમીન પર મહત્તમ સમક્ષિતિજ અંતર સુધી ફેલાવી શકાય ?View Solution
- 3એક પ્રયોગમાં એક નાનો સ્ટીલનો બોલ પ્રવાહીમાં $10\, cm/s$ ની અચળ ઝડપથી પડે છે. જો બૉલને ઉપર તેના અસરકારક વજનથી બમણા બળથી ખેચવામાં આવે તો તે ....... $cm/s$ ઝડપથી ઉપર ગતિ કરશે?View Solution
- 4પાણીની સપાટીથી વસ્તુને $2\, km$ ઊંડાઇએ રાખતા તેના કદમાં થતો ફેરફાર $\frac{\Delta V }{ V }=1.36\, \%,$ હોય તો તેના કદ પ્રતિબળ અને કદ વિકૃતિ નો ગુણોત્તર કેટલો થાય?[પાણીની ઘનતા $=1000\, kg m ^{-3}$ અને $\left. g =9.8 \,ms ^{-2} .\right]$View Solution
- 5${V_0}$ કદ અને ${d_0}$ ઘનતા ધરાવતો પદાર્થ $d$ ઘનતા ધરાવતા પ્રવાહી પર મૂકતાં કેટલામો ભાગ બહાર રહે?View Solution
- 6$0.3\,g$ દળ અને $8\,g / cc$ જેટલી ધનતા ધરાવતા એક નાના બોલનું જ્યારે ગ્લિસરીન ભરેલા પાત્રમાં પતન કરવામાં આવે છે તો અમુક સમય બાદ તેના વેગ અચળ થઈ જાય છે. જો ગ્લિસરીનની ધનતા $1.3\,g / cc$ હોય તો બોલ પર પ્રવર્તતું સ્ગિન્ધ બળ $x \times 10^{-4}\,N$ હશે . [g $:=10 m / s ^2$ લો.]View Solution
- 7$r$ ત્રિજયાનો એક નાનો ગોળો સ્થિર સ્થિતિમાંથી એક સ્નિગ્દ્ય પ્રવાહીમાં પડે છે. સ્નિગ્દ્ય બળના પરીણામે ઉષ્મા ઉત્પન્ન થાય છે. જયારે આ ગોળો તેની ટર્મીનલ વેગ પ્રાપ્ત કરશે, ત્યારે ઉષ્મા ઉત્પન્ન થવાનો દર ......... ને ચલે છે.View Solution
- 8પાત્રમાં $H$ ઊંચાઇ સુધી પાણી ભરેલ છે.પાત્રના તળિયે છિદ્ર પાડતાં ${T_1}$ સમયમાં પાણી $\frac{H}{\eta }\,(\eta > 1)$ ઊંચાઇ સુધી થાય છે.હવે બાકીનું પાણી ખાલી થતાં લાગતો સમય ${T_2}$ છે,જો${T_1} = {T_2}$ હોય,તો $\eta =$ ____View Solution
- 9નળાકાર પાત્રમાં પ્રવાહી ભરેલ છે.જયારે પાત્રને તેના અક્ષને અનુલક્ષીને ફેરવવામાં આવે છે.પ્રવાહી તેની બાજુ પર ચડે છે.પાત્રની ત્રિજયા $ r $ અને પાત્રની કોણીય આવૃતિ $\omega $ પરિભ્રમણ/સેકન્ડ છે. કેન્દ્ર અને બાજુ પરના પ્રવાહીની ઊંચાઇનો તફાવત કેટલો થાય?View Solution
- 10View Solutionસાચું બર્નોલીનું સમીકરણ. . . . . . .છે. (સંજ્ઞાઓ તેમનો પ્રમાણિત અર્થ રજૂ કરે છે.)
