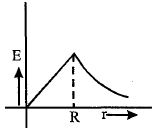
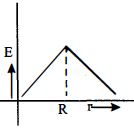
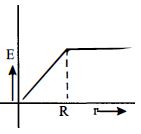
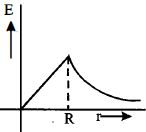
આકૃતિમાં દર્શાવ્યા પ્રમાણે $R$ ત્રિજ્યાના વર્તુળાકાર ક્ષેત્રફળમાં કાગળના સમતલની અંદરની દિશામાં એકસમાન ચુંબકીયક્ષેત્ર પ્રવર્તે છે અને તેનું મૂલ્ય અચળ દરથી વધે છે. આ માટે ઉત્પન્ન થતું વિદ્યુતક્ષેત્ર $E(r)$ નો $r$ ની સાથેનો આલેખ કેવો મળે?
- A
- B
- C
- D
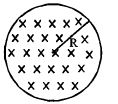
JEE MAIN 2014, Diffcult
Download our app for free and get started
a
Inside the sphere field varies linearly i.e., \(E \propto r\) with distance and outside varies according to \(E \propto \frac{1}{{{r^2}}}\) Hence the variation is shown by curve \((a)\)
Inside the sphere field varies linearly i.e., \(E \propto r\) with distance and outside varies according to \(E \propto \frac{1}{{{r^2}}}\) Hence the variation is shown by curve \((a)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionટ્રાન્સફોર્મરનો કોર લેમીનેટેડ કરવાથી...
- 2કોઇલમાં પ્રવાહ $8\, A$ થી $2 \,A$ , $ 3 \times {10^{ - 2}} $ $second$ માં કરતાં $2\, V$ $emf$ ઉત્પન્ન થાય છે.તો કોઇલનું આત્મપ્રેરકત્વ કેટલું થાય? (in $millihenry$)View Solution
- 3$1 \,m$ લાંબા ધાત્વીય સુવાહકને તેના એક છેડાથી $5 \,rad s ^{-1}$ ના કોણીય વેગથી શિરોલંબ રીતે ઉર્ધ્વ સમતલમાં પૂર્વ-પશ્ચિમ દિશાને સમાંતર ભ્રમણ કરાવવામાં આવ છે. જો પૃથ્વીના યુંબકત્વની સમક્ષિતિજ ઘટક $0.2 \times 10^{-4} \,T$ હોય તો વાહકના બે છેડાઓ વચ્ચે પ્રેરિત સરેરાશ $emf$ ........ હશે.View Solution
- 4$\frac{10}{\sqrt{\pi}}\,cm$ ત્રિજ્યાની વર્તુળાકાર વાહક લૂપને $0.5\,T$ મૂલ્યના સમાન ચુંબકીયક્ષેત્રમાં લંબરૂપે મૂકવામાં આવે છે. ચુંબકીય ક્ષેત્રનું મૂલ્ય અચળ દરે ધટીને $0.5\,s$ માં શૂન્ય બને છે. તો $0.25\,s$ વખતે વર્તુળાકાર લૂપમાં પ્રેરિત થતું વીજચાલક બળView Solution
- 5ગતિશાસ્ત્રમાં વેગમાન $ m \times \,v $ ને વિદ્યુતશાસ્ત્રમાં કઇ રીતે દર્શાવાય?View Solution
- 6ટ્રાન્સફોર્મરના પ્રાથમિક ગૂંચળામાં આંટાની સંખ્યા $140$ અને ગૌણ આંટાની સંખ્યા $280$ છે,પ્રાથમિક ગૂંચળામાં પ્રવાહ $4\, A$ હોય તો ગૌણ ગૂચળામાં વહેતો પ્રવાહ ($A$ માં) કેટલો હશે?View Solution
- 7View Solutionઆપેલ પરિપથ માટે, વપરાયેલ ટ્રાન્સફોર્મર માટે પ્રતિક્રિયા આપો :
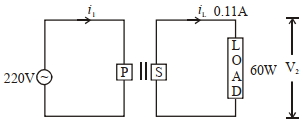
- 8એક આંટો ધરાવતી $a$ બાજુવાળી ચોરસ લૂપને બીજા $b(b \gg a)$ બાજુવાળી ચોરસ લૂપની અંદર સમકેન્દ્રિય રીતે મુકેલ છે. જો $b$ બાજુવાળી ચોરસ લૂપની અંદર $I$ પ્રવાહ પસાર કરવામાં આવે તો આ બંને લૂપ વચ્ચેનું અન્યોન્ય પ્રેરકત્વ કેટલું થાય?View Solution
- 9View Solutionઆપેલ પરિપથમાં બલ્બ અચાનક પ્રકાશિત થશે જો ....
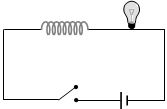
- 10View Solutionજ્યારે બે ગુચળાને એકબીજાની નજીક રાખવામા આવે ત્યારે તેમની જોડનું અન્યોન્ય પ્રેરકત્વ કોના પર આધાર રાખે?