As we know,
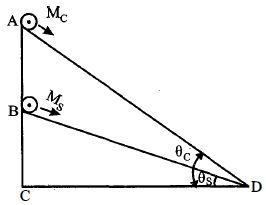
Acceleration, \(a = \frac{{mg\sin \theta }}{{m + \frac{I}{{{r^2}}}}}\)
\(\begin{array}{l}
\,For\,cylinder,\,{a_c} = \frac{{{M_c}g.\sin {\theta _c}}}{{{M_c} + \frac{1}{2}\frac{{{M_c}{R^2}}}{{{R^2}}}}}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{M_c}g.\sin {\theta _c}}}{{{M_c} + \frac{{{M_c}{R^2}}}{{2{R^2}}}}}
\end{array}\)
\(\begin{array}{l}
or,\,\,\,{a_c} = \frac{2}{3}g\sin \,{\theta _c}\\
\,\,\,\,\,\,\,\,For\,sphere,\\
\,\,\,\,\,{a_s} = \frac{{{M_s}g\sin {\theta _s}}}{{{M_s} + \frac{{{I_s}}}{{{r^2}}}}}\\
\,\,\,\,\,\,\,\,\,\,\, = \frac{{{M_s}g\sin {\theta _s}}}{{{M_s} + \frac{2}{5}\frac{{M{R^2}}}{{{R^2}}}}}
\end{array}\)
\(\begin{array}{l}
or,\,\,\,\,\,\,\,{a_s} = \frac{5}{7}g\sin {\theta _s}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,given,\,{a_c} = {a_s}\\
i.e.,\,\,\frac{2}{3}g\sin {\theta _c} = \frac{5}{7}g\sin {\theta _s}\\
\therefore \,\,\frac{{\sin {\theta _c}}}{{\sin {\theta _s}}} = \frac{{\frac{5}{7}g}}{{\frac{2}{3}g}} = \frac{{15}}{{14}}
\end{array}\)
Download our appand get started for free
Similar Questions
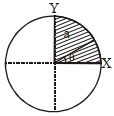
- 1$M$ દળના અને $r$ ત્રિજ્યાની નિયમિત અર્ધ-વર્તૂળાકાર તકતીમાં કેન્દ્રમાંથી પસાર થતી અને સમતલને લંબ રેખા પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 2$\theta = at + b{t^2} + c{t^3}$ મુજબ કોણીય અંતર ફરે તો તેનો કોણીય પ્રવેગ કેટલો થાય ?View Solution
- 3એક પાતળી વર્તુળાકાર રિંગ જેનું દળ $M$ અને ત્રિજ્યા $R$ તેની ધરી પર અચળ કોણીય વેગ $\omega $ થી પરિભ્રમણ કરે છે. રિંગનાં વ્યાસના બિંદુઓ પર $m$ દળનાં એવા બે પદાર્થોને ધીમેથી જોડવામાં આવે છે. હવે રિંગ કેટલા કોણીય વેગથી ગતિ કરશે?View Solution
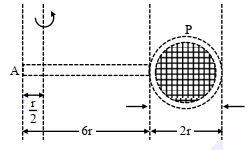
- 4આકૃતિમાં એક બેડમિન્ટન રેકેટના પરિમાણ આપેલા છે. જો બેડમિન્ટનના રેખીય અને વર્તુળાકાર ભાગનું સમાન દળ $(M)$ અને દોરીનું દળ અવગણ્ય હોય તો, હેન્ડલના બિંદુ $A$ થી $\frac{r}{2}$ અંતરે રેકેટના હેન્ડલને લંબ અને રિંગના સમતલમાં રહેલી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા ....... $Mr^2$ જેટલી થાય?View Solution
- 5View Solutionતંત્રને સમતોલન સ્થિતિમાં રાખવા માટે તેના પર લાગતા ટોર્કને સંતુલિત કરવું પડે . આ વિધાન સાચું કરવા માટે ટોર્ક ક્યાં લેવું પડે ?
- 6$L$ લંબાઈ ધરાવતા અરેખીય ઘનતા ધરાવતા સળિયાની ઘનતા $\rho(\mathrm{x})={a}+{b}\left(\frac{\mathrm{x}}{\mathrm{L}}\right)^{2}$ મુજબ આપવામાં આવે છે જ્યાં $a$ અને $ {b}$ અચળાંક અને $0 \leq \mathrm{x} \leq \mathrm{L}$ છે.સળિયાના દ્રવ્યમાન કેન્દ્ર માટે $x$ નું મૂલ્ય કેટલું હોવું જોઈએ?View Solution
- 7$1\ m$ ત્રિજયા અને $4\ kg$ દળ ધરાવતી તકતી સમક્ષિતિજ સમતલમાં ગબડે છે. જો તેના દ્રવ્યમાન કેન્દ્રની ઝડપ $10\ cm/sec$ હોય,તો તેની ચાકગતિ ઊર્જાView Solution
- 8ફલાય વ્હીલ સ્થિર સ્થિતિમાંથી $3.0\ rad/sec^2$ ના અચળ કોણીય પ્રવેગથી ચાકગતિ કરે છે. અવલોકનકાર નોંધે છે કે તે $ 4.0\ sec$ ના સમયગાળામાં $120\ radian$ નો ખૂણો આંતરે છે. અવલોકનકાર અવલોકનની શરૂઆત કરે છે તો ....... $(\sec)$ સમય સુધી વ્હીલ ભ્રમણ કરશે .View Solution
- 9સમાન દળ અને સમાન જાડાઇની તકતીની ઘનતાનો ગુણોત્તર $1:3$ છે.તો તેની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રાનો ગુણોત્તર કેટલો થાય?View Solution
- 10આકૃતિમાં $M$ દળ અને $\sigma$ દળ ઘનતા ધરાવતી તકતી દર્શાવેલ છે. આકૃતિમાં રેખાંકિત કરેલ તકતીના ચૌથા ભાગના દ્રવ્યમાન કેન્દ્રના યામ $\frac{x}{3} \frac{a}{\pi}, \frac{x}{3} \frac{a}{\pi}$ હોય તો તો $x$નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું હશે?$[ a=$ રેખાંકિત કરેલ ભાગનું ક્ષેત્રફળ$]$View Solution