આકૃતિમાં $q_1$ અને $q_2$ બે વિદ્યુતભારને કારણે વિદ્યુતક્ષેત્રરેખા દર્શાવે છે. બે વિદ્યુતભારની સંજ્ઞા કેવી હશે?
AIPMT 1994, Easy
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$4.9 \times 10^{5} \;N / C$ મૂલ્ય ધરાવતું શિરોલંબ વિદ્યુતક્ષેત્ર, $0.1 \,g$ દળ ધરાવતા પાણીના બુંદને નીચે પડતું આટકાવવા પૂરતું છે. બુંદ પરનો વિધુતભાર........$ \times 10^{-9} \;C$ હશેView Solution
[$g =9.8 \,m / s ^{2}$ આપેલા ]
- 2સમાન વિરૂદ્ધ નિશાની ધરાવતી પૃષ્ઠ વિદ્યુતભાર ઘનતા ($\sigma$ $= 26.4 \times 10^{-12} \ C/m^2$) વાળી બે સમાંતર વિશાળ પાતળી ધાતુની તકતી છે. આ તકતી વચ્ચેનું વિદ્યુતક્ષેત્ર ........$N/C$ છે.View Solution
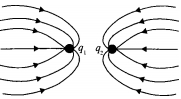
- 3$2 \,m$ અંતરે રહેલા બે સમાન વિદ્યુતભાર $q$ ધરાવતા બે સ્થિર કણની વચ્ચે એક $1 \,{mg}$ દળ અને $q$ વિદ્યુતભાર ધરાવતો કણ પડેલો છે. જો મુક્ત વિદ્યુતભારને તેના સમતોલન સ્થાનેથી $x\;(x\, < 1\, {m})$ જેટલું થોડુક સ્થાનાંતર કરવવામાં આવે, તો કણ સરળ આવર્ત ગતિ કરે છે. જો ${q}^{2}=10\, {C}^{2}$ હોય તો આ દોલનોની કોણીય આવૃતિ $....\,\times 10^{8}\, {rad} / {s}$ થાય.View Solution
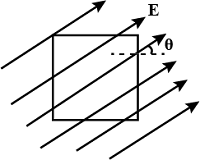
- 4આકૃતિમાં દર્શાવ્યા મુજબ $L$ મીટર બાજુવાળો એક ચોરસ સપાટીને પેપરના સમતલમાં ચોરસની સમક્ષિતિજ બાજુ સાથે $\theta$ ખૂણે $\vec E\;(V/m)$ જેટલા સમાન વિદ્યુતક્ષેત્રમાં મુકેલ છે, તો પૃષ્ઠ સાથે સંકળાયેલ ફલક્સ $volt \;m $ એકમમાં કેટલું થાય?View Solution
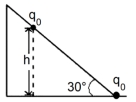
- 5આકૃતિ માં દર્શાવ્યા પ્રમાણે બે બિંદ્દુવત વીજભાર $\left( q _0=+2 \mu C \right)$ એક ઢોળાવ (ઢળતા સમતલ) ઉપર રાખવામાં આવેલ છે. દરેક બિંદ્દુવત વીજભારનું દળ $20\,g$ છે. એવું ધારો કે વિદ્યુતભાર અને ઢોળાવ વચ્ચે ધર્ષણબળ પ્રવર્તતું નથી. બે બિંદુવત્ત વિદ્યુતભારોથી બનેલું તંત્ર $h =x \times 10^{-3}\,m$ ઊંચાઇએ, સમતોલન અવસ્થામાં રહે છે. $x$ નું મૂલ્ય ....... થશે.View Solution
$\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9\,N m ^2\,C ^{-2}, g=10\,m s ^{-2}\right)$
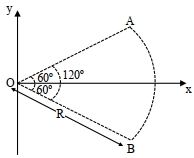
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે સળિયા ${AB}$ ને $120^{\circ}$ ના ખૂણે વાળીને $R$ ત્રિજયાની છાપ બનાવવામાં આવે છે. $(-Q)$ વિદ્યુતભારને સળિયા $AB$ પર સમાન રીતે વિતરિત કરેલ છે. તેના કેન્દ્ર $O$ પર વિદ્યુતક્ષેત્ર $\overrightarrow{{E}}$ કેટલું હશે?View Solution
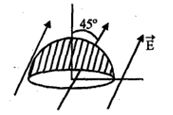
- 7સમક્ષિતિજ સમતલમાં તેની અંદરની બાજુની રેખા પર કોઈ વિદ્યુતભાર ન હોય તેવો $a$ ત્રિજ્યાનો સમતલ સપાટી વાળો એક અર્ધ ગોળો છે. તેની શિરોલંબ દિશા સાથે $\pi /4$ ખૂણો બનાવે તેમ સમાન વિદ્યુતક્ષેત્ર આવેલું છે. અર્ધ ગોળાની વક્ર સપાટીમાંથી પસાર થતું વિદ્યુત ફલક્સ ....... છે.View Solution
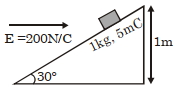
- 8આકૃતિમાં દર્શાવ્યા મુજબ $200 \, \frac{ N }{ C }$ સમાન સમક્ષિતીજ વિદ્યુત ક્ષેત્રમાં મૂકેલ ઢળતી સપાટી, સમક્ષિતીજ સાથે $30^{\circ}$ નો કોણ રચે છે. $1\, kg$ દળ અને $5\, mC$ વિજભાર ધરાવતા પદાર્થને આ ઢળતી સપાટી $1\, m$ ઊંચાઈ વિરામ સ્થાનેથી સરકવા દેવામાં આવે છે. જો ઘર્ષણાંક $0.2$ હોય તો તળીયે પહોંચવા માટે લીધેલો સમય શોધો.($s$ માં)View Solution
$\left[ g =9.8 \,m / s ^{2}, \sin 30^{\circ}=\frac{1}{2}\right.$; $\left.\cos 30^{\circ}=\frac{\sqrt{3}}{2}\right]$
- 9$10^{-4} \mathrm{~m}^2$ આડછેદનું ક્ષેત્રફળ ધરાવતા પાતળા ધાતુના તારનો $30 \mathrm{~cm}$ ત્રિજયાની વલય બનાવવામાં ઉપયોગ થાય છે. $2 \pi \mathrm{C}$ મૂલ્યનો ધન વીજભાર સમાન રીતે વલય પર વિતરીત થયેલ છે જ્યારે $30 \mathrm{pC}$ મૂલ્યનો ધન વીજભાર વલયના કેન્દ્ર પર રાખેલ છે. વલયમાં ઉદભવતું તણાવબળ_____$\mathrm{N}$ છે કે જેને લીધે વલયમાં વિકૃતિ ઉદ્ભવતી નથી. (ગુરૂત્વીય અસર અવગણો)$\left(\right.$ ને, $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9 \mathrm{SI}$ એકમ $)$View Solution
- 10બંધ પૃષ્ઠની અંદરની બાજુએ $20\ \mu C$ નો વિદ્યુતભાર મૂકવામાં આવે તો પૃષ્ઠ સાથે સંકળાયેલ ફલક્સ છે. જો $\, 80\ \mu C$ બંને વિદ્યુતભાર પૃષ્ઠની અંદરની બાજુએ ઉમેરવામાં આવે તો ફલક્સમાં થતો ફેરફાર....... છે.View Solution