આપેલ ગોળીય પૃષ્ઠમાંથી પસાર થતું વિદ્યુતક્ષેત્રના ફલ્કસ ગણતરી કરવા માટે લીધેલ વિદ્યુતક્ષેત્ર કયાં વિદ્યુતભારોના કારણે ઉત્પન્ન થશે?
IIT 2004, Easy
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
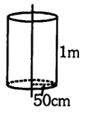
- 1$1\, mm$ ત્રિજ્યાના લાંબા સુરેખ તાર પર વિદ્યુતભાર સમાન રીતે વિતરિત થયેલો છે. તારની પ્રતિ $cm$ લંબાઈ $Q$ દીઠ વિદ્યુતભાર $Q$ કુલંબ છે. $50\, cm$ ત્રિજ્યા અને $1\, m$ લંબાઈના તારથી સંમિત રીતે ઘેરાયેલો છે. નળાકાર ના પૃષ્ઠમાંથી પસાર થતું કુલ ફલક્સ .......... છે.View Solution
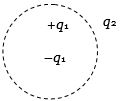
- 2ક્રમિક $ + Q$ અને $ - Q$ વિજભાર ધરાવતા બે બિંદુવત વિજભારો $A$ અને $B$ ને એક બીજાથી નિયત અંતર પર અલગ રાખેલ છે કે જેથી તેમના વચ્ચે લાગતું બળ $F$ છે. જો $A$ નો $25\%$ વિજભાર $B$ પર ટ્રાન્સફર કરવામાં આવે, તો આ વિજભારો વચ્ચે લાગતું બળ કેટલું થશે?View Solution
- 3$2 L \times 2 L \times L$ પરિણામાણ ધરાવતા લંબધનમાં $4 L ^2$ ક્ષેત્રફળ ધરાવતા પૃષ્ઠ $s$ ના કેન્દ્રસ્થાને વિદ્યુતભાર $q$ મૂકવામાં આવે તો $s$ ના સામેના પૃષ્ઠમાંથી પસાર થતું ફલફસView Solution
- 4$\sigma$ પૃષ્ઠ ઘનતા ધરાવતી એકસમાન રીતે વિદ્યુતભારિત કરેલ $R$ ત્રિજ્યાની તકતીને ${xy}$ સમતલમાં ટકતીનું કેન્દ્ર ઉગમબિંદુ પર રહે તેમ મૂકેલી છે. તો $z-$ અક્ષ પર ઉગમબિંદુથી $Z$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતા કેટલી હશે?View Solution
- 5$R$ ત્રિજ્યા ધરાવતા એક ગોલીય કવચ પર નિયમિત પૃષ્ઠ વીજભાર ઘનતા $\sigma$ છે. ગોલીય કવચની સપાટી ઉપર કોઈ પણ બિંદુ આગળ વિદ્યુતક્ષેત્ર. . . . . થશે.View Solution
- 6$10\ cm$ ત્રિજયા ધરાવતા ગોળાથી $20\ cm$ અંતરે વિદ્યુતક્ષેત્ર $100\ V/m$ છે.તો કેન્દ્રથી $3\ cm$ અંતરે વિદ્યુતક્ષેત્ર કેટલા .....$V/m$ થાય?View Solution
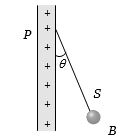
- 7આકૃતીમાં દર્શાવ્યા મુજબ મોટી વિદ્યુતભારીત પ્લેટ $P$ સાથે બાંધેલી દોરી $S$ બે બોલ $B$ ને ખૂણો બને તે રીતે લટકાવેલ છે તો પ્લેટની વિદ્યુતભારની પૃષ્ઠ ઘનતા કોના સમપ્રમાણમાં છે?View Solution
- 8$R$ ત્રિજ્યાના અને અનંત લંબાઈના વિદ્યુતભાર વિતરણ વાળા નળાકારને લીધે વિદ્યુતક્ષેત્ર શોધો અને તેની પાસે રેખીય વિદ્યુતભાર ઘનતા $\lambda$ છે. જે તેના અક્ષથી અડધી ત્રિજ્યા આગળ મળે છે.View Solution
- 9$10\,cm$ બાજુવાળા સમબાજુ ત્રિકોણ $ABC$ ના શિરોબિંદુ પર અનુક્રમે $1\,\mu C$ , $-1\,\mu C$ અને $2\,\mu C$ વિદ્યુતભાર મૂકતાં $C$ પર રહેલ વિદ્યુતભાર પર કેટલા .....$N$ બળ લાગે?View Solution
- 10$q$ વિદ્યુતભાર સાથે $r\, (r < R)$ ના વિદ્યુતભારીત ગોળીય વાહકના કેન્દ્રથી $r$ (અંતરે $R$) આવેલા બિંદુ આગળ વિદ્યુતક્ષેત્રની તીવ્રતા ....... હશે.View Solution