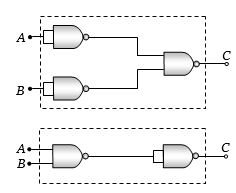
આપેલ પરિપથ રહેલ $NAND$ ગેટના સંયોજનથી મળતા ગેટ અનુક્રમે કયા હશે?

Medium
a
(a) \(C = \overline {\bar A.\bar B} = \overline {\bar A + \bar B} = A + B\) (De morgan’s theorem)
Hence output \(C\) is equivalent to \(OR\) gate
\(C = \overline {\overline {AB} .\overline {AB} } = \overline {\overline {AB} + \overline {AB} } = AB + AB = AB\)
In this case output \(C\) is equivalent to \(AND\) gate.
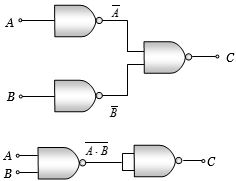
(a) \(C = \overline {\bar A.\bar B} = \overline {\bar A + \bar B} = A + B\) (De morgan’s theorem)
Hence output \(C\) is equivalent to \(OR\) gate
\(C = \overline {\overline {AB} .\overline {AB} } = \overline {\overline {AB} + \overline {AB} } = AB + AB = AB\)
In this case output \(C\) is equivalent to \(AND\) gate.

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
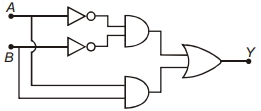
- 1View Solutionઆપેલ આકૃતિનાં જોડાણ માટે બુલીયન સમીકરણ લખો.
- 2ક્યો $pn$ જંક્શન રીવર્સ બાયસમાં ઉપયોગ થતો નથી ?View Solution
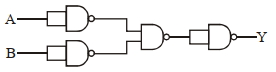
- 3View Solutionનીચે દર્શાવેલ પરિપથ ..... ને સમતુલ્ય છે.
- 4$P-N$ જંકશનનો પોટેન્શિયલ બેરિયર $0.6 V$ છે.ડિપ્લેશન સ્તરની જાડાઇ $1\mu m$ છે,તો વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
- 5નીચે આપેલ ટ્રુથ ટેબલ કયા ગેટ માટેનું છે?View Solution
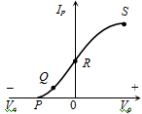
$A$ $B$ $Y$ $0$ $0$ $0$ $0$ $1$ $1$ $1$ $0$ $1$ $1$ $1$ $1$ - 6View Solutionટ્રાયોડની પ્રેરીત લાક્ષણિકતામાં કયું બિંદુ કટ-ઓફ વોલ્ટેજ દર્શાવે છે.
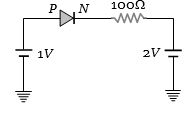
- 7આપેલ પરિપથમાં રહેલ આદર્શ $P- N $ જંકશનમાંથી કેટલા ....$mA$ પ્રવાહ પસાર થાય?View Solution
- 8View Solutionટ્રાન્ઝીસ્ટરનો પાતળામાં પાતળો ભાગ . . . . . .
- 9જ્યારે $P - N$ જંકશન રીવર્સ બાયસમાં આવે ત્યારે જંકશનમાંથી પસાર થતો પ્રવાહ મોટે ભાગે .......ના કારણે આવે છે.View Solution
- 10વિધાન $-1$ : શુધ્ધ અર્ધવાહક માટે અવરોધનો તાપમાનગુણાંક ઋણ હોય છેView Solution
વિધાન $-2$ : તાપમાંન વધારતા કન્ડકશન બેન્ડમાં વધારે વિજભાર વાહકો મુક્ત થાય છે
