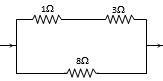
Resistance of series combination of \(3\,\Omega \) and \(1\,\Omega \) is
\(R_{1}=3+1=4 \,\Omega, R_{2}=8\, \Omega\)
Let \(i\) be the total current in the circuit.
Current through \(R_{1}\) is \(i_{1}=\frac{i \times R_{2}}{R_{1}+R_{2}}=\frac{i \times 8}{12}=\frac{2 i}{3}\)
Current through \(R_{2}\) is \(i_{2}=\frac{i \times R_{1}}{R_{1}+R_{2}}=\frac{i \times 4}{12}=\frac{i}{3}\)
Power dissipated in \(3\, \Omega\) resistor is
\(P_{1}=i_{1}^{2} \times 3\) ....\((i)\)
Power dissipated in \(8 \Omega\) resistor is
\(P_{2}=i_{2}^{2} \times 8\) ....\((ii)\)
\(\therefore \quad \frac{P_{1}}{P_{2}}=\frac{i_{1}^{2} \times 3}{i_{2}^{2} \times 8}\) or, \(\frac{P_{1}}{P_{2}}=\frac{(2 i / 3)^{2} \times 3}{(i / 3)^{2} \times 8}=\frac{12}{8}=\frac{3}{2}\)
\(P_{1}=\frac{3}{2} \times P_{2}=\frac{3}{2} \times 2=3 \,\text { watt }\)
\(\therefore\) Power dissipated across \(3 \Omega\) resistor is \(3\,watt.\)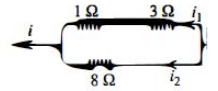
Download our appand get started for free
Similar Questions
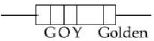
- 1View Solutionએક કાર્બન અવરોધ નિમ્ન વર્ણ સંકેતો ધરાવે છે. આ અવરોધનું મૂલ્ય શું છે?
- 2ત્રણ સમાન બેટરી $L$ લંબાઇના તાર સાથે શ્રેણીમાં જોડતા,તેના તાપમાનમાં $t$ સમયમાં $T$ જેટલો વઘારો થાય છે. $N$ બેટરીને સમાન દ્રવ્યના બનેલા $2L$ લંબાઇના તાર સાથે જોડતા,તેના તાપમાનમાં $t$ સમયમાં $T$ જેટલો વઘારો થાય છે તો $N$ = ...............View Solution
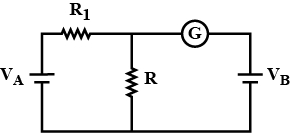
- 3આપેલ પરિપથમાં રહેલ કોષ $A$ અને $B$ નો અવરોધ નહિવત છે. $V _{ A }=12\; V , R _{1}=500\; \Omega$ અને $R =100\; \Omega$ માટે ગેલ્વેનોમીટર $(G)$ આવર્તન બતાવતું નથી તો $V_{B}$ નું મૂલ્ય .... $V$ હશેView Solution
- 4પોટેન્શિયોમિટરના પ્રયોગમા કોઇ એક વિદ્યુતકોષ માટે તટસ્થ બિંદુ $240 \,cm$ અંતર મળે છે.આ વિદ્યુતકોષને સમાંતર $2Ω$ નો અવરોધ જોડતાં તટસ્થ બિંદુ $120 \,cm$ અંતરે મળે છે.આ વિદ્યુતકોષનો આંતરિક અવરોધ કેટલા ................ $\Omega $ થાય?View Solution
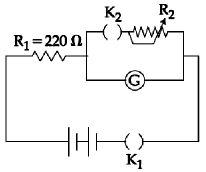
- 5જ્યારે કળ $K_1$ બંધ હોય અને $K_2$ ખુલ્લી હોય ત્યારે ગેલ્વેનોમીટરનું આવર્તન $\theta_0$ બરાબર છે (આકૃતિ જુઓ). $K_2$ ને પણ બંધ કરતા તથા $R_2$ ને $5\,\Omega $ ગોઠાવતાં ગેલ્વેનોમીટરમાં આવર્તન $\frac{{\theta _0}}{5}$ થાય છે. તો આ ગેલ્વેનોમીટરનો અવરોધ કેટલા ............ $\Omega$ હશે? (બેટરીનો આંતરિક અવરોધ અવગણો).View Solution
- 6$2\,V\ e.m.f$ ધરાવતા દરેક એકસમાન ચાર કોષોને સમાંતરમાં જોડેલા છે. જે સમાંતરમાં જોડેલા $15 \,\Omega$ ના બે અવરોધો ધરાવતા બાહ્ય પરિપથને વિધુતપ્રવાહ પહોચાડે છે. સમતુલ્ય કોષનો ટર્મિનલ વોલ્ટેજ આદર્શ વોલ્ટમીટર દ્વારા માપવામાં આવતા તે $1.6\ V$ છે. તો દરેક કોષનો આંતરિક અવરોધ ............. $\Omega$ ગણો.View Solution
- 7$0\,^oC$ તાપમાને પ્લેટીનીયમ અવરોધ થર્મોમીટરમાં કોઈલનો અવરોધ $5$ ઓહમ છે $100\,^oC$ અને તાપમાને $5.75$ ઓહમ છે. અજ્ઞાત તાપમાને તેનો અવરોધ $5.15 $ ઓહમ છે. તો અજ્ઞાત તાપમાન ............ $^oC$ હશે.View Solution
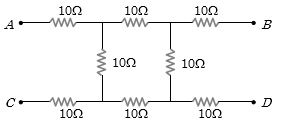
- 8આપેલ પરિપથમાં બે બિંદુઓ $A$ અને $D$ વચ્ચેનો સમતુલ્ય અવરોઘ ($\Omega$ માં) કેટલો થાય?View Solution
- 9$1\, m$ લંબાઈ અને $5\,\Omega$ અવરોધના એક પ્રાથમિક પોટેન્શિયોમીટર સાથે $4 \,V\, emf$ ની એક બેટરી અને શ્રેણી અવરોધ $R$ જોડેલ છે. આ પોટેન્શિયોમીટરના તાર પર $10\,cm$ એ $5\, mV$ વિજસ્થિતિમાનનો તફાવત આપે તેવું $R$ નું મૂલ્ય ............... $\Omega$ હશે.View Solution
- 10જ્યારે $4\,A$ જેટલો પ્રવાહ પસાર થાય છે ત્યારે એેક અવરોધમાં $10\,s$ માં $H$ મૂલ્યની ઉષ્મીય ઊર્જા ઉત્પન્ન થાય છે.જો પ્રવાહ વધારીને $16\,A$ કરવામાં આવે તો અવરોધમાં $10\,s$માં ઉત્પન્ન થતી ઉષ્મીય ઊર્જા $.......\,H$ થશે.View Solution
