$0\,^oC$ તાપમાને પ્લેટીનીયમ અવરોધ થર્મોમીટરમાં કોઈલનો અવરોધ $5$ ઓહમ છે $100\,^oC$ અને તાપમાને $5.75$ ઓહમ છે. અજ્ઞાત તાપમાને તેનો અવરોધ $5.15 $ ઓહમ છે. તો અજ્ઞાત તાપમાન ............ $^oC$ હશે.
Medium
Download our app for free and get started
d
\(R\,\, = \,\,{R_0}\,(1 + \alpha \theta )\,\)
\(R\,\, = \,\,{R_0}\,(1 + \alpha \theta )\,\)
\( \Rightarrow \,\,\alpha \,\, = \,\,\frac{{R - {R_0}}}{{{R_0}\theta }}\)
\([\,\because \,\,R\,\, = \,\,5.75\,\,\Omega \,,\,\,{R_0} = \,\,5\,\Omega \,,\) \(q\,\, = \,\,{100\,^o}C\,,\) \(R'\,\, = \,\,5.15\,\,\Omega ]\,\)
\(\alpha \,\, = \,\,\,\frac{{5.75 - 5}}{{5\,\, \times \,\,100}}\,\,\) \( = \,\,0.15\,\, \times \,\,{10^{ - 2}}\,\,per{\,\,^o }C\)
\(\theta '\,\, = \,\,\frac{{R' - {R_0}}}{{{R_0}\alpha }}\,\,\) \( = \,\,\frac{{5.15 - 5}}{{5\,\, \times \,\,0.15\,\, \times \,\,{{10}^{ - 2}}}}\)
\(=\frac{0.15}{5\times 0.15\times {{10}^{-2}}}={{20}^{}}\,^{o}C\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ઇલેકિટ્રક કીટલી ને $220\ V$ લગાડતાં તેમાંથી $4\ A$ પ્રવાહ વહે છે.આ કીટલીમાં ભરેલ $1\ kg $ પાણીને $20\,^o C$ થી ઊકળતા કેટલા ................ $min$ સમય લાગશે? પાણીનું ઉત્કલનબિદુ $100^o C$ છે.View Solution
- 2દરેક બાજુનો $3\, \Omega$ અવરોધ ધરાવતા ચોરસ આકારના તારને વાળીને વર્તુળ બનનાવામાં આવે છે. વર્તુળના વ્યાસના બિંદુ વચ્ચેનો અવરોધ $\Omega$ ના એકમમાં કેટલો થાય?View Solution
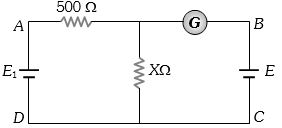
- 3આપેલ પરિપથમાં બેટરી $E_1$ નો $e.m.f.$ $=12\; V$ અને શૂન્ય આંતરિક અવરોધ જ્યારે બેટરી $E$ નો $e.m.f.$ $=2\; V$ છે. જો ગેલ્વેનોમીટરનું અવલોકન શૂન્ય હોય,તો અવરોધ $X $ નું મૂલ્ય કેટલું હશે?View Solution
- 4$120\, V, 10\, \Omega $ ઘરાવતી બેટરી સાથે સમાંતરમાં $50\, W -100 \,V$ ના મહતમ કેટલા બલ્બ જોડવાથી તે મહતમ તીવ્રતાથી પ્રકાશિત થાય?View Solution
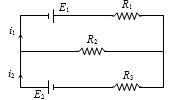
- 5આપેલ પરિપથમાં $E_1 = 4\,V$, $R_1 = 2\,\Omega$ $E_2 = 6\,V$, $R_2 = 2$ $\Omega $, $R_3 = 4\,\Omega $ હોય તો પ્રવાહ $ i_1 $ નું મૂલ્ય કેટલા .............. $A$ થાય?View Solution
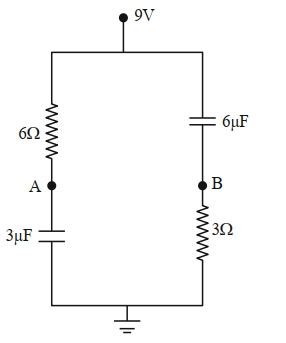
- 6જ્યારે બિંદુઓ $A$ અને $B$ ને તાર વડે જોડવામાં આવે ત્યારે આપેલ આકૃતિમાં $6 \mu F$ સંધારકમાં સંગ્રહિત વિદ્યુતભાર______$\mu C$ છ.View Solution
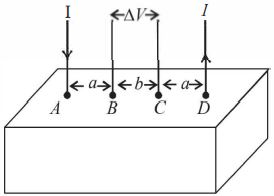
- 7આકૃતિમાં દર્શાવ્યા પ્રમાણેનાં $\rho $ અવરોધકતાનાં વાહક દ્રવ્યને એક ચોસલો ધારો. વિદ્યુત પ્રવાહ $I, A$ આગળ દાખલ થાય છે $D$ આગળથી છોડે (બહાર નીકળે) છે. $B$ અને $C$ વચ્ચે ઉદભવતાં વોલ્ટેજ $\Delta V$ શોધવા સંપાતપણા સિદ્ધાંત લાગુ પાડવામાં આવે છે. નીચેના ક્રમમાં ગણત્રી કરવામાં આવે છે.View Solution
$[A]$ $A$ માંથી દાખલ થતો વિદ્યુત પ્રવાહ $I$ લો અને ચોસલામાં તે એક અર્ધ ગોળાકાર સપાટી ઉપર પ્રસરે છે. તેમ માનવામાં આવે.
$[B]$ઓહમને નિયમ $E = \rho j $ ને ઉપયાગ કરીને $A$ થી $r$ અંતરે વિદ્યુત ક્ષેત્ર $E (r)$ ગણવામાં આવે જ્યાં $j,r$ આગળ દર એકમ ક્ષેત્રફળે વિદ્યુત પ્રવાહ છે.
$[C]$ $E (r)$ નાં $r$ પરનાં આધારપણા પરથી $r$ આગળ સ્થિતિમાન $V (r)$ મેળવવામાં આવે.
$[D]$$D$ માંથી મહાર નીકળતા ($D$ ને છોડતા) વિદ્યુત પ્રવાહ $ I$ માટે $(i)$ અથવા
$B$ અને $C$ વચ્ચે માપવામાં આવતો $\Delta V$ ............ થાય.
- 8ઓપન સર્કિટ કોષનો વિદ્યુતસ્થિતિમાનનો તફાવત $2.2\, volts$ છે. જ્યારે તેના બે ઈલેક્ટ્રોડ વચ્ચે $4\, ohm$ નો અવરોધ જોડવામાં આવે તો આ વિદ્યુતસ્થિતિમાનનો તફાવત $2\, volts$ થાય છે. તો કોષનો આંતરિક અવરોધ ( $ohm$ માં) કેટલો હશે?View Solution
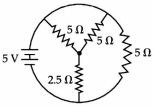
- 9$5 \,V$ બેટરી વડે (આકૃતિમાં દર્શાવ્યા અનુસાર) પરિપથને પ્રાપ્ત થતો કુલ પ્રવાહ........$A$ હશે.View Solution
- 10વિધાન $-1 :$ સ્વિચ $ON$ કરતી વખતે બલ્બ ફ્યુજ થવાની શક્યતા મહત્તમ હોય.View Solution
વિધાન $-2 : $ જ્યારે બલ્બ બંધ હોય ત્યારે તેનો અવરોધ બલ્બ ચાલુ ત્યારના અવરોધ કરતાં ઘણો નાનો હોય છે.