આપેલ પરિપથમાં $A$ અને $B$ વચ્ચેનું સમતુલ્ય કેપેસીટન્સ $\mu F$ માં કેટલું થાય?
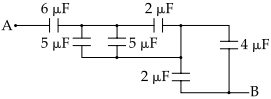

JEE MAIN 2018, Diffcult
d
The simplified circuit of the circuit given in question as follows:
The simplified circuit of the circuit given in question as follows:
The equivalent capacitance between \(C \& D\) capacitors of \(2\, \mu \mathrm{F}, 5\, \mu \mathrm{F}\) and \(5\, \mu \mathrm{F}\) are in parallel.
\(\therefore \mathrm{C}_{\mathrm{CD}}=2+5+5=12 \,\mu \mathrm{F}\)
(\(\because\) In parallel grouping \(C_{e q}=C_{1}+C_{2}+\ldots .+C_{n})\)
Similarly equivalent capacitance between \(\mathrm{E}\) \(\& \mathrm{BC}_{\mathrm{EB}}\)
\(=4+2=6\, \mu \mathrm{F}\)
Now equivalent capacitance between \(A \& B\)
\(\frac{1}{C_{e q}}=\frac{1}{6}+\frac{1}{12}+\frac{1}{6}=\frac{5}{12}\)
\(\Rightarrow \mathrm{C}_{\mathrm{eq}}=\frac{12}{5}=24\, \mu \mathrm{F}\)
(\(\because \) In series group-ing, \(\frac{1}{{{C_{eq}}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + \ldots \ldots + \frac{1}{{{C_n}}}\)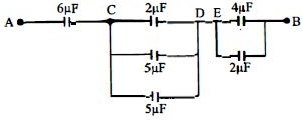
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વિદ્યુતસ્થિતિમાન $V = 6x - 8x{y^2} - 8y + 6yz - 4{z^2}$ હોય,તો ઉદ્ગમ બિંદુ પર મૂકેલાં $2\,C$ વિદ્યુતભાર પર કેટલા ......$N$ બળ લાગે?View Solution
- 2$\alpha-$કણ અને એક પ્રોટોનને સમાન સ્થિતિમાનના તફાવતથી વિરામ સ્થિતિમાંથી પ્રવેગિત કરવામાં આવે છે. બંને દ્વારા પ્રાપ્ત કરેલ રેખીય વેગમાનોનો ગુણોત્તર $..........$ થશે.View Solution
- 3સમાંતર પ્લેટ કેપેસિટરમાં અનુક્રમે $K_1$ અને $ K_2$ ડાઈ ઈલેકટ્રીક અચળાંક સાથે $t_1$ અને $t_2$ જાડાના સ્તરો મૂકવામાં આવે છે તો આ સંગ્રાહકની કેપેસિટી કેટલી ?View Solution
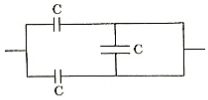
- 4View Solutionઆકૃતિમાં દર્શાવેલ સંયોજન માટે સમતુલ્ય સંધારકતા ..... છે.
- 5$3\,\mu F$ અને $5\,\mu F$ ધરાવતા કેપેસિટરને અનુક્રમે $300\,V$ અને $500\,V$ ચાર્જ કરેલ છે.બંનેને તાર વડે જોડતાં તે કેટલી ઊર્જા ગુમાવશે?View Solution
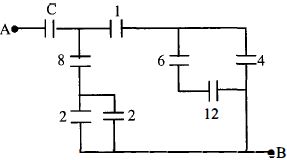
- 6આકૃતિમાં કેપેસીટરનો પરિપથ આપેલ છે જેમાં બધા કેપેસીટરના મૂલ્યો માઇક્રોફેરાડે માં છે જો $A$ અને $B$ વચ્ચેનો સમતુલ્ય કેપેસીટન્સ $1\,\mu F$ હોય તો $C$ નું મૂલ્ય કેટલું હશે?View Solution
- 7પૃૃષ્ઠ $A$ અને $B$ સમાન સ્થિતિમાન $V'$ આગળ છે. $A$ થી $B$ સમાન તરફ ગતિમાન વિદ્યુતભારને ગતિ કરતાં થતું કાર્ય ........ છે.View Solution

- 8હવામાં ગોળાકારની કેપેસિટિ $50 \,\mu F$ છે. અને તેને તેલમાં ડૂબડતાં તે બને $110 \,\mu F$ છે. તો તેલનો ડાઈ ઈલેકટ્રીક ગણો.View Solution
- 9$10\ \mu F$ મૂલ્ય ધરાવતા બે કેપેસિટરોના સમાંતર જોડાણને $200 \,volt\, dc$ થી વિદ્યુતભારીત કરવામાં આવે તો જૂલમાં સંગ્રહિત ઊર્જા કેટલી હશે ?View Solution
- 10$4 \,\mu F$ ના કેપેસિટરને $50\,V$ સુધી ચાર્જ કરીને $100\,V$ ધરાવતા $2\,\mu F$ ના કેપેસિટર સાથે જોડવામાં આવે છે.તો જોડાણ પહેલાની ઊર્જા અને જોડાણ પછીની ઊર્જા ના મૂલ્યો $(10^{-2}\,J) $ ના ગુણાકારમાં કેટલા થાય?View Solution
