આપેલ ટ્રાન્ઝિસ્ટર સંતૃપ્ત વિભાગમાં કાર્ય કરે તો $V _{ BB }$ નું મૂલ્ય (વોલ્ટ માં) કેટલું હશે?
$( R _{\text {out }}=200 \Omega, R _{\text {in }}=100 k \Omega,$$ V _{ cC }=3 volt , V _{ BE }=0.7 volt ,V _{ GE }=0, \beta=200 )$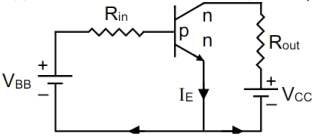
AIIMS 2019, Diffcult
Download our app for free and get started
c
Consider the given figure.
Consider the given figure.
From the above figure,
\(V _{ CE }= V _{ CC }- I _{ C } R _{0}\)
\(0=3- I _{ C }(200)\)
\(I _{ C }=\frac{3}{200}\)
\(=15 \,mA\)
As we know that,
\(\beta=\frac{I_{C}}{ I _{B}}\)
\(I_{B}=\frac{15 mA }{200}\)
\(=75 \mu A\)
Therefore,
\(V _{ BE }= V _{ BB }- I _{ B } R _{ in }\)
\(V _{ BB }=0.7+\left(75 \times 10^{-6}\right)\left(100 \times 10^{3}\right)\)
\(=8.2 V\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
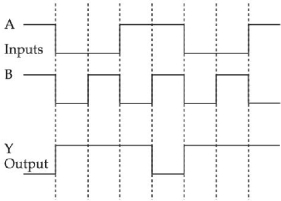
- 1બે ઈનપુટ $A$ અને $B$ ધરાવતા લોજીક પરિપથ માટેના આઉટપુટ $(Y)$ માટે સાચો લોજીક પરિપથ શોધોView Solution
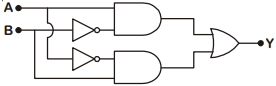
- 2નીચે આપેલ ગેટ્સની ગોઠવણમાં ઇનપુટ $A$ અને $ B$ ના પદોમાં આઉટપુટ $Y$ ને કઈ રીતે તરીકે દર્શાવી શકાય?View Solution
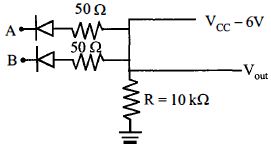
- 3પરિપથમાં $A$ અને $B$ ઈનપુટ ટર્મિનલ છે. લૉજિક $1\, = \,> 5\, V$ લૉજિક $0\, =\, < 1\, V$. આપેલ પરિપથ કયા લૉજિક ગેટ તરીકે વર્તશે?View Solution
- 4શુદ્ધ સિલિકોનના સેમ્પલમાં $10^{13} atom/cm^3 $ જેટલામાં ફોસ્ફરસ મિશ્ર કરવામાં આવે છે. જો બધા ડોનર અણુઓ સક્રિય હોય અને ઈલેક્ટ્રોનની મોબિલીટી $1200 cm^2/ volt$ $sec$ હોય તો $20° C $ એ અવરોધકતા કેટલા ......$\Omega$ $cm$ હશે?View Solution
- 5ટ્રાયોડ જેનું આત્મ વાહકત્વ $2.5 m A/volt$ અને એનોડનો અવરોધ $20 kilo ohm$ છે તેને ઍમ્પ્લિફાયર તરીકે ઉપયોગમાં લેવામાં આવે $10$ છે. જેનું એમ્પ્લીકેશનના તો પ્લેટ પરીપથ સાથે જોડેલ અવરોધ.....$ k\,\Omega$View Solution
- 6$P -N$ જંકશનમાં..View Solution
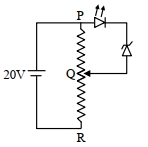
- 7એક સ્થિતિમાન વિભાજક પરિપથને $20 \mathrm{~V}$ ના $DC$ ઉદગમ, $1.8 \mathrm{~V}$ પર પ્રકાશિત થતી $LED$ (લાઈટ એમિંટિંગ ડાયોડ) અને $3.2 \mathrm{~V}$ બ્રેક ડાઉન વોલ્ટેનના ઝેનર ડાયોડ સાથે જોડવામાં આવે છે. અવરોધક તાર ($PR$) ની લંબાઈ $20 \mathrm{~cm}$છે. $PQ$ ની ન્યૂનતમ લંબાઈ જેને લીધે $LED$ પ્રકાશીત થવાની શરૂ કરે તે. . . . . . $\mathrm{cm}$ છે.View Solution
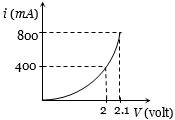
- 8આકૃતિમાં $P - N$ જંકશન ડાયોડની ફૉરવર્ડ બાયસ લાક્ષણિકતા દર્શાવી છે. આ ડાયોડને $2\;V$ ઇનપુટ વૉલ્ટેજ આપતાં આશરે તેનો ડાયનેમિક અવરોધ કેટલા .........$\Omega$ હશે ?View Solution
- 9ટ્રાન્ઝિસ્ટરના $CB$ મોડમાં જ્યારે કલેક્ટર વોલ્ટેજ $0.5$ વોલ્ટેજ જેટલો તફાવત થાય છે. ત્યારે કલેક્ટર પ્રવાહ $0.05mA$ જેટલો બદલાય છે તો, આઉટપુટ અવરોધ કેટલા .......$k\,\Omega$ હશે ?View Solution
- 10જાંબલી રંગ (તરંગલંબાઈ=$4000 \mathring A)$ નાં $LED$ બનાવવા માટે અર્ધવાહક દ્રવ્યનો $......eV$ જેટલો ઊર્જાનો બેન્ડગેપ હશે.(નજીક્તમ પૂર્ણાંક માટે લખો)View Solution