અલગ દળ, ત્રિજ્યા અને ધનતા ધરાવતા બે નક્કર ગોળાઓ એક ખરબચડા ઢોળાવ ઉપર થી સમાન સ્થિતિ હેઠળ નીચે ગબડે છે. તેમનો નીચે આવવા નો સમય તેમના થી સ્વતંત્ર છે.
Medium
d
(d)
(d)
For rolling down an inclined plane,
\(a_{c m}=\frac{g \sin \theta}{1+\frac{1}{m R^2}}\)
For 5 phere of mass \(m\) and radius \(R, 1=\frac{2}{5} m R^2\)
So, \(\quad a_{c u}=\frac{g \sin 0}{1-\frac{2}{5}\left({m R^2}^2\right)}=\frac{5}{7} g \sin 0\)
As acceleration of centre of mass of rolling body only depends upon angle of inclination,
So, time taken to come down, \(t =\sqrt{\frac{2 L}{a_{c h}}}\)
\(\left(\because L=\frac{1}{2} a_{c n} t^2\right)\)
\(t=\sqrt{\frac{2 L \times 7}{5 g \sin \theta}}=\sqrt{\frac{14 L}{5 g \sin \theta}}\), where \(L=\) length of inclined plane.
Here, \(t\) is independent of mass, radius and density of spheres. Option (d) is correct.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
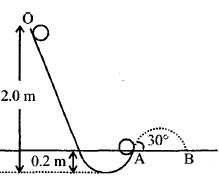
- 1એક ટેનિસ બોલ (પોલું ગોળીય કવચ) ટેકરી પર $O$ થી શરૂ કરીને નીચે તરફ દડે છે. બિંદુ $A$ પાસે દડો હવામાં ઊછળવાની શરૂઆત સમક્ષિતિજ સાથે $30^o$ ના ખૂણેથી કરે છે. $B$ પાસે દડો જમીન પર પહોચે છે. તો અંતર $AB$ ની કિંમત ......... $m$ થાય. ( દળ $m$ અને ત્રિજ્યા $R$ વાળા પોલા ગોળીય કવચની તેના વ્યાસને અનુલક્ષીને જડત્વની ચાકમાત્રા $= \frac {2}{3}\,mR^2$)View Solution
- 2$W$ જેટલું વજન ધરાવતો એક ભારે લોખંડનો સળિયો, તેનો એક છેડો જમીન ઉપર અને બીજો છેડો માણસના ખભા ઉપર રાખે છે. સળિયો સમક્ષિતિજ સાથે $\theta$ કોણ રચે છે. માણસ દ્વારા અનુભવાનું વજન ............. થશે.View Solution
- 3$r$ નળાકારની ફરતે દોરડું વીંટાળેલું છે અને જડત્વની ચાકમાત્રા $ I $ છે. દોરીના એક છેડે $m $ દળ જોડેલો છે. તેની સમક્ષિતિજ અક્ષ પર મુક્તપણે ભ્રમણ કરી શકે છે. જો $ m$ દળને $h$ ઊચાઈ એથી સ્થિતિમાંથી મુક્ત કરવામાં આવે ત્યારે તેના વેગ કેટલો થશે ?View Solution
- 4View Solutionકોઈ બાહ્ય ટોર્ક ની ગેરહાજરી માં જ્યારે એક પદ્રાર્થ તેની અક્ષ ઉપર ભ્રમણ કરી રહ્યો હોય તો નીચેના માંથી ખોટું નિવેદન પસંદ કરો.
- 5View Solutionકણ નિયમિત વર્તૂળાકાર ગતિ કરે છે. વર્તૂળના સમતલના કયાં બિંદુએ કણનું કોણીય વેગમાનનું સંરક્ષણ થશે ?
- 6બે તકતીમાંથી એકની ઘનતા $7.2\ g / cm^3$ અને બીજીની ઘનતા $8.9\ g/cm^3$ છે. આ બંનેના દળ અને જાડાઈ સરખી છે. તો તેમની જડત્વની ચાકમાત્રાનો ગુણોત્તર શોધો.View Solution
- 7$l$ લંબાઈના ચોરસના ચારે ખૂણા પર $m $ દળના પદાર્થ મૂકેલા છે.તો ચોરસના સમતલને લંબ અને તેના કેન્દ્રમાથી પસાર થતી અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજયા કેટલી થાય?View Solution
- 8બળ $\mathop {\text{F}}\limits^ \to \,\, = \,\,2\hat i\,\, + \;\,\hat j\,\, + \;4\hat k\,$ અને $ \mathop r\limits^ \to \,\, = \,\,7\hat i\,\, + \;3\hat j\,\, + \;\,\hat k\,$ બિંદુ આગળ ટોર્ક ...... હોય.View Solution
- 9કોઈ પદાર્થ પર ટોર્ક લગાવ્યા વગર, પરંતુ જડત્વની ચાકમાત્રા માં ફેરફાર થવાથી તેની કોણીય ઝડપ ${\omega _1}$ માથી ${\omega _2}$ થાય છે. તો બંને કિસ્સામાં ચક્રાવર્તનની ત્રિજ્યાનો ગુણોત્તર શું થશે?View Solution
- 10એક પૈડાને $1000\ N-m$ નું ટોર્ક આપતા તે તેના કેન્દ્રમાંથી પસાર થતા અક્ષની આસપાસ $200\ kg-m^2$ જડત્વની ચાકમાત્રા સાથે ફરે છે. તો $3 $ સેકન્ડ પછી પૈડાનો કોણીય વેગ $=$ ......... $\ rad/s$View Solution
