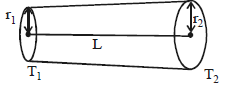Let \(T_s\) be the temperature of the surroundings.
According to \(Newton's\) law of cooling
\(\frac{{{T_1} - {T_2}}}{t} = K\left( {\frac{{{T_1} + {T_2}}}{2} - {T_s}} \right)\)
For first \(5\,minutes,\)
\({T_1} = {70^ \circ }C,{T_2} = {60^ \circ }C,t = 5\,minutes\)
\(\therefore \frac{{70 - 60}}{5} = K\left( {\frac{{70 + 60}}{2} - {T_s}} \right)\)
\(\frac{{10}}{5} = K\left( {65 - {T_s}} \right)\) \(...(i)\)
For next \(5\,minutes\)
\({T_1} = {60^ \circ }C,{T_2} = {54^ \circ }C,t = 5 minutes\)
\(\therefore \frac{{60 - 54}}{5} = K\left( {\frac{{60 + 54}}{2} - {T_s}} \right)\)
\(\frac{6}{5} = K\left( {57 - {T_s}} \right)\) \(...(ii)\)
Divide eqn. \((i)\) by eqn. \((ii)\) , we get
\(\frac{5}{3} = \frac{{65 - {T_s}}}{{57 - {T_s}}}\)
\(285 - 5{T_s} = 195 - 3{T_s}\)
\(2{T_s} = 90\,\,or\,\,{T_s} = {45^ \circ }C\)
Download our appand get started for free
Similar Questions
- 1બે સમાન ક્ષેત્રફળ વાળી પ્લેટને એકબીજાના સંપર્કમાં રાખેલી છે. તેમની જાડાઈ $2.0\,\, cm$ અને $5.0 \,\,cm$ છે. પહેલી પ્લેટની બાહ્ય સપાટીનું તાપમાન $-20°C$ અને બીજી પ્લેટની બાહ્ય સપાટીનું તાપમાન $20°C$ છે. જ્યારે તેમની ઉષ્મા વાહકતાનો ગુણોત્તર $2:5$ હોય તો સંપર્કમાં રહેલી સપાટીનું તાપમાન ........ $^oC$ શોધો.View Solution
- 2View Solutionરેડીયેેશન ઉર્જાનો દર એ ગરમ પદાર્થ માટે મહત્તમ હોય છે જ્યારે સપાટી
- 3ત્રણ તકતી $ A$ ,$B$ અને $C$ ની ત્રિજયા અનુક્રમે $2\;m,4\;m$ એ $6\;m$ છે.તેમાંથી ઉત્સર્જન થતી મહત્તમ તરંગલંબાઇ $ 300\;nm ,400\;nm$ અને $500\;nm$ છે.તેમના ઉત્સર્જન પાવર $Q_a, Q_b$ અને $Q_c$ છે.તોView Solution
- 4બે સમાન પદાર્થોના તાપમાન $ {727^o}C $ અને $ {327^o}C $ છે,તો ઉત્સર્જન ઊર્જાનો ગુણોત્તર કેટલો થાય?View Solution
- 5જો સ્પેક્ટ્રલ ઉત્સર્જન પાવરને $y$-અક્ષ ઉપર અને તરંગ લંબાઈ $x$-અક્ષ પર દોરવામાં આવે તો વળાંક નીચેનો વિસ્તાર અને તરંગલંબાઈની ઉપરનો ભાગ એView Solution
- 6View Solutionસારો શોષક એ સારો ઉત્સર્જક હોય છે.તે કયાં નિયમનું વિધાન છે.
- 7View Solutionએક પદાર્થ પર કાળો ડાધ છે.તેને ગરમ કરીને અંધારીયા રૂમમાં લઇ જતાં તે તેજસ્વી દેખાય છે.તેનું કારણ
- 8દિવાલના બે સ્તર $A$ અને $B$ જુદા જુદા પદાર્થના બનેલા છે. બંને સ્તરની જાડાઈ સમાન છે. $A,$ $K_A = 3 K_B$ છે. ઉષ્મીય સંતુલન દિવાલના છેડે તાપમાનનો તફાવત $20°C$ છે. $A$ ના છેડે તાપમાનનો તફાવત ..... $^oC$ શોધો.View Solution
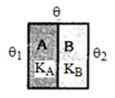
- 9સ્લેબ સમાન જાડાઈના કોપર અને બ્રાસના બે સમાંતર સ્તર છે અને ઉષ્મીય વાહકતા $1:4$ ના ગુણોત્તર છે. જો બ્રાસની મુક્ત બાજુનું તાપમાન $100°C$ અને કોપરનું $0°C$ છે. તો અત:બાજુનું તાપમાન ....... $^oC$ છે.View Solution
- 10આકૃતિમાં દર્શાવેલ સળિયા માટે ઉષ્માવહનનો દર કેટલો હશે? ($T_2 > T_1$ અને સળિયાના દ્રવ્યની ઉષ્માવાહકતા $K$ છે)View Solution