અવાહક દિવાલવાળા પાત્રના વાલ્વવાળા વિભાજક દ્વારા બે સમાન ભાગ પાડેલા છે. એક ભાગમાં $P$ દબાણ અને $T$ તાપમાને આદર્શ વાયુ ભરેલો છે. જ્યારે બીજા ભાગને શૂન્યવકાશિત કરેલો છે. જો વાલ્વ અચાનક ખોલી નાખવામાં આવે, તો વાયુનું દબાણ અને તાપમાન કેટલા થશે?
AIEEE 2011, Medium
Download our app for free and get started
a
It is the free expansion Internal energy of the gas remains constant, hence
It is the free expansion Internal energy of the gas remains constant, hence
\(T_{2}=T\)
Using at constant temperature,
\(P_{1} V_{1}=P_{2} V_{2}\)
\(P_{2}=\frac{P}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે વાયુના તાપમાન,દબાણ અને કદ અનુક્રમે $T, P$ અને $V $ છે,તેમનું મિશ્રણ કરવાથી કદ $ V $ અને તાપમાન $T$ છે,તો નવું દબાણ અને દળView Solution
- 2$T$ તાપમાન માટે એક પરમાણ્વિક વાયુ માટે $\bar v , \bar v_{rms}$ અને $v_p$ અનુક્રમે સરેરાશ ઝડપ, $rms$ ઝડપ અને મહત્તમ શક્ય ઝડપ છે. અણુનું દળ $m$ હોય તો .....View Solution
- 3કોઈ વાયુનો $27°C$ ઓરડાના તાપમાને $rms$ વેગ $ 412 m/s$ મળે છે. આ વાયુનું નામ......છે.View Solution
- 4View Solutionઆપેલ આકૃતિ માં પહાડની ટોચ ઉપર અને નીચે ઘનતાનો ગુણોતર કેટલો થાય?
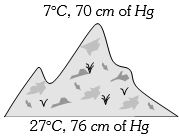
- 5આપેલ તાપમાને $m$ દળના વાયુની $rms$ ઝડપ કોના સમપ્રમાણમાં હોય ?View Solution
- 6$T$ તાપમાન માટે એક પરમાણ્વિક વાયુ માટે $\bar v , \bar v_{rms}$ અને $v_p$ અનુક્રમે સરેરાશ ઝડપ, $rms$ ઝડપ અને મહત્તમ શક્ય ઝડપ છે. અણુનું દળ $m$ હોય તો .....View Solution
- 7View Solutionવિધાન : વાયુ માટે સરેરાશ મુક્તપથ ઘનતાના વ્યસ્ત પ્રમાણમા હોય છે
કારણ : વાયુ માટે સરેરાશ મુક્તપથ દબાણના વ્યસ્ત પ્રમાણમા હોય છે
- 8ચોક્કસ વાયુના અણુઓનો $STP$ એ સરેરાશ મુક્ત પથ $1500\,d$ છે, જ્યાં $d$ એ વાયુના અણુઓનો વ્યાસ છે. પ્રમાણભૂત દબાણ જાળવી રાખતા, $ 373\,K$ પર અંદાજિત સરેરાશ મુક્ત પથ સરેરાશ ........... $d$ છે.View Solution
- 9View Solutionવાયુને ગરમ કરતાં પિસ્ટન
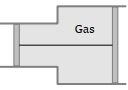
- 10પાત્રમાં $m$ દળ ધરાવતા $N$ અણુઓ વાયુ $A$ ના અને $2m$ દળ ધરાવતા $2N$ અણુઓ વાયુ $B$ ના ભરેલા છે.વાયુ $A$ ના x-ઘટકના વેગના વર્ગનો સરેરાશ $ {w^2} $ અને વાયુ $B$ નો વેગના વર્ગનો સરેરાશ $ {v^2} $ હોય,તો $ \frac{{{w^2}}}{{{v^2}}} $View Solution