અવરોધનો તાપમાન ગુણાંક $0.00125\,^oC$ છે.$300\, K$ તાપમાને અવરોધ $1\,\Omega$ છે.તો ........... $K$ તાપમાને અવરોધ $2\,\Omega $ થાય?
IIT 1980, Medium
d
તાપમાન \(300\, K \) = \((300 - 273)\,^o\) સે = \(27\,^o\) સે
તાપમાન \(300\, K \) = \((300 - 273)\,^o\) સે = \(27\,^o\) સે
\(R_{27} = R_0[1 + 0.00125(27)] = 1\) …… \((1)\)
ધારો કે, તાપમાને અવરોધ \(2\,\Omega\) થાય છે
\(R_t = R_0[1 + 0.00125(t)] = 2\) ……. \((2)\)
સમીકરણ \((1)\) અને \((2)\) નો ગુણોતર લેતાં,
\(\frac{1}{2}\,\, = \,\,\frac{{{R_0}[1 + \,\,0.00125(27)]}}{{{R_0}\,\,[1\,\, + \,\,0.00125(t)]}}\)
\(\,\therefore \,\,1\,\, + \,\,0.00125t\,\, = \,\,2[1\,\, + \,\,0.00125(27)]\)
\(t = 854\,^o\) સે = \((854 + 273)\,K = 1127\, K\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
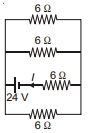
- 1આકૃતિમાં દર્શાવેલ પરિપથમાં વિદ્યુતપ્રવાહ $I$ $.......A$ છે.View Solution
- 2નીચે બે વિધાનો આપેલા છે એકને કથન $A$ અને બીજાને કારણે $R$ થી દર્શાવેલ છે.View Solution
કથન $A$ : કોન્સ્ટન્ટન મેગ્નેનીન જેવી મિશ્ર ધાતુઓ પ્રમાણિત અવરોધના ગૂંચળા બનાવવા માટે વપરાય છે.
કારણ $R$ : કોન્સ્ટન્ટન અને મેગ્નેનીનને ખૂબ જ નાનો તાપીય પ્રસરણાંક હોય છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
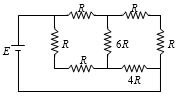
- 3આપેલ તંત્રમાં $4\, \Omega$ આંતરિક અવરોઘ ઘરાવતી બેટરીમાંથી મહતમ પાવર મેળવવા માટે $R $ નું કેટલા ............. $\Omega$ હોવું જોઈએ?View Solution
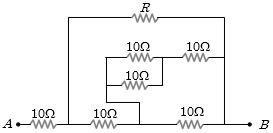
- 4આપેલ પરિપથમાં $A$ અને $B$ બિંદુ વચ્ચેનો સમતુલ્ય અવરોધ $18\,Ω$ થવા માટે $R$ નું મૂલ્ય કેટલા ............... $\Omega$ હોવું જોઈએ?View Solution
- 5બે વાયરો $A$ અને $B$ સમાન ધાતુ અને સમાન દળ ધરાવે છે. વાયર $A$ ની ત્રિજ્યા વાયર $B$ ની ત્રિજ્યા કરતા બમણી છે. તો જ્યારે વાયર $A$ તથા $B$ ને સમાંતરમાં જોડવામાં આવે તો કુલ અવરોધ.... હશે.View Solution
- 6$200\, {W},\;100 \,{V}$ ના રેટિંગ ધરાવતા બલ્બને $200\, {V}$ ના ઉદગમ સાથે જોડેલ છે. કેટલા મૂલ્યના ($\Omega$ માં) $R$ અવરોધને તેની સાથે શ્રેણીમાં જોડાવો જોઈએ કે જેથી બલ્બ સમાન પાવર આપે?View Solution
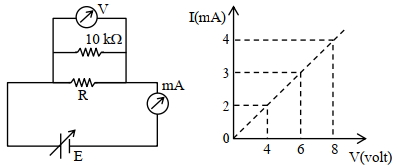
- 7અવરોધ $(R)$ માપવા માટે નીચે મુજબ પરિપથ રચવામાં આવે છે. આ પરિપથ માટે $V-I$ લાક્ષણિકતા માટે વોલ્ટમીટર અને એમીટરના અવલોકનોનો દર્શાવ્યા મુજબનો આલેખ મળ છે. $R$નું મૂલ્ય ........ $\Omega$ છે.View Solution
- 8$20\,A$ પ્રવાહ ધરાવતા અને $3.14 \times 10^{-6}\,m ^2$ આડછેદ ક્ષેત્રફળના સિલ્વર વાયરમાં ઈલેક્ટ્રોનનો ડ્રિફ્ટ વેગ શોધો. $Ag$ નો અણુભાર $=108$, સિલ્વરના ઘનતા $=10.5 \times 10^3\,kg / m ^3..........\times 10^{-4} m / sec$.View Solution
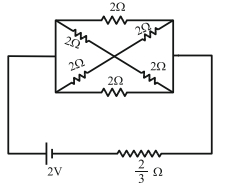
- 9નીચે દર્શાવેલ વિદ્યુત પરિપથમાં બેટરીનું emf $2 \mathrm{~V}$ અને આંતરિક અવરોધ $\frac{2}{3} \Omega$ છે. તો આ સંપૂર્ણ વિદ્યુત પરિપથમાં વપરાતો વિદ્યુત પાવર ...... $W$View Solution
- 10ઓપન સર્કિટ સ્થિતિમાં એક વિદ્યુતકોધના બે ધ્રુવોં વચ્યેનો સ્થિતિમાનનો તફાવત $2.2\; V$ છે. તેની સાથે $R = 5\,\Omega $ નો અવરોધ જોડતા આ સ્થિતિમાનનો તફાવત $1.8 \;V$ બને છે. તો આ કોષનો આંતરિક અવરોધ $(r)$ ....... $\Omega$ હશે?View Solution
