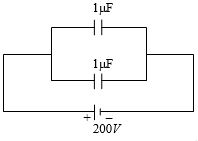
બે અલગ કરેલી (અવાહકીય) પ્લેટોને સમાન રીતે એવી રીતે વિદ્યુતભારીત કરેલ છે. કે જેથી તેમની વચ્ચેનો સ્થિતિમાન તફાવત $V_2$ - $V_1$ = $20\ V$. પ્લેટ $2$ ઉંચા સ્થિતિમાન છે. પ્લેટોને $= 0.1\ m$ અંતરે અલગ કરેલી અનંત રીત વિશાળ (વિસ્તૃત) ગણી શકાય છે. પ્લેટ $1$ ની અંદરની પસાર પર સ્થિત સ્થિતિએ રહેલા એક ઈલેકટ્રોનને મુક્ત કરવામાં આવે છે. જે જ્યારે પ્લેટને અથડાય ત્યારે તેની ઝડપ કેટલી છે.
$ (e = 1.6 × 10^{-19}\ C, m_0= 9.11 × 10^{-31}\ kg)$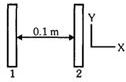
Medium
Download our app for free and get started
a
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$1$ જેટલો ડાઈઈલેક્ટ્રીક અચળાંક ધરાવતા અવાહકથી બનેલો સાધન ગોળો નિયમિત રીતે ચાર્જ કરવામાં આવ્યો છે. જો અનંત અંતરે સ્થિતિમાન શૂન્ય છે તેમ ધારી લઈએ તો તેની સપાટીએ $V$ સ્થિતિમાન શૂન્ય લઈએ તો તેના કેન્દ્ર પર કેટલો સ્થિતિમાન મળશે?View Solution
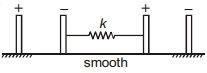
- 2ચાર્જ થયેલા બે કેપેસીટરની બહારની પ્લેટો સ્થિત એટલે કે ન હલી શકે તેવી છે અને અંદરની પ્લેટોની ' $k$ ' જેટલા બળ અચળાંક ધરાવતી સ્પ્રિંગ વડે જોડેલ છે. બંને કેપેસીટર પર $q$ જેટલો ચાર્જ રહેલ છે. તો સંતુલિત અવસ્થામાં સ્પ્રિંગની લંબાઈમાં થતો વધારો કેટલો થશે ?View Solution
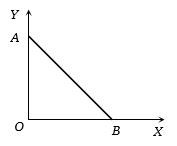
- 3આકૃતિમાં દર્શાવ્યા મુજબ $+q$ વિદ્યુતભારને ઉગમબિંદુ $O$ પર મૂકેલો છે. બિંદુ $A \,(0,a) $ આગળથી $-Q$ વિદ્યુતભારને બિંદુ $B\,(a,0)$ પર સુરેખ માર્ગ $AB$ એ લઇ જવા કેટલું કાર્ય કરવું પડે?View Solution
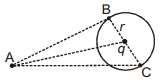
- 4$r$ ત્રિજ્યાવાળા વર્તુળના કેન્દ્ર પર $q$ જેટલો ચાર્જ રાખેલ છે, $B$ અને $C$ બિંદુઓ આ વર્તુંળના પરિઘ પર છે. જ્યારે બિંદુ $A$ આ વર્તુળથી બહાર છે. જો $W_{A B}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $B$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે અને $W_{A C}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $C$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે તો આપેલી આકૃતિ માટે કયું વિધાન સત્ય છે ?View Solution
- 5$64$ મરક્યુરીના ટીપા દરેકને $10\, V$ સુધી વિદ્યુતભારીત કરેલ છે. તેમને ભેગા કરીને એક મોટુ બુંદ બનાવવામાં આવે છે તો આ બુંદનો વિદ્યુત સ્થીતીમાન........$V$View Solution
- 6બે અલગ અલગ $\frac{2}{3} R$ અને $\frac{1}{3} R$ ત્રિજ્યા ધરાવતા $S_{1}$ અને $S_{2}$ વાહક ગોળા પર અનુક્રમે $12\, \mu C$ અને $-3\, \mu C$ જેટલો વિજભાર છે અને બંને એકબીજાથી ખૂબ જ લાંબા અંતરે છે. તેને હવે એક વાહક તારથી જોડેલા છે. તેના પછી લાંબા સમયે $S_{1}$ અને $S_{2}$ પરનો વિજભાર કેટલો હશે?View Solution
- 7View Solutionકેપેસિટરની પ્લેટો વચ્ચે એલ્યુમિનિયમ પાતળી શીટ વચ્ચે મુકવામાં આવેલ છે, તો કેપેસિટરનું કેપેસીટન્સ
- 8પ્લેટોની વચ્ચે હવાનું માધ્યમ ધરાવતા સમાંતર પ્લેટ કેપેસિટરનું કેપેસિટન્સ $9\ pF$ છે. પ્લેટો વચ્ચેનું અંતર $'d'$ છે. હવે પ્લેટોની વચ્ચેની જગ્યાને ડાય-ઈલેકટ્રીક વડે ભરવામાં આવે છે. જેમાં એક ડાઈ ઈલેકટ્રીક પાસે $ K_1 = 3$ અને ડાઈ ઈલેકટ્રીક અચળાંક અને જાડાઈ $d$ છે. જ્યારે બીજા પાસે ડાઈ ઈલેકટ્રીક અચળાંક $K_2 = 6$ અને જાડાઈ $2d/3$ છે. તો હવે, કેપેસિટરનું કેસિટન્સ ......$pF$ શોધો.View Solution
- 9અવકાશનાં એકક્ષેત્રમાં નિયમિત વિદ્યુતક્ષેત્ર $\vec{E}=10 \hat{i}( V / m )$ લાગુ પડે છે. જો કોઈ ધન વિદ્યુતભારને $\bar{v}=-2 \hat{j}$, જેટલા વેગથી તેમાંથી પસાર થાય તો તેની સ્થિતિઊર્જા કેવી થશે?View Solution
- 10આપેલ તંત્રની કુલ ઊર્જા કેટલા........$joules$ થાય?View Solution
